功率因数计算公式_功率因数与什么有关_提高功率因数的方法

　　功率因数（Power Factor）的大小与电路的负荷性质有关， 如白炽灯泡、电阻炉等电阻负荷的功率因数为1，一般具有电感性负载的电路功率因数都小于1。功率因数是电力系统的一个重要的技术数据。功率因数是衡量电气设备效率高低的一个系数。功率因数低，说明电路用于交变磁场转换的无功功率大， 从而降低了设备的利用率，增加了线路供电损失。

　　在交流电路中，电压与电流之间的相位差（Φ）的余弦叫做功率因数，用符号cosΦ表示，在数值上，功率因数是有功功率和视在功率的比值，即cosΦ=P/S.

　　功率因数计算公式

　　自从交流电机取得应用至今日，功率因数和位移因数在很多场合被混淆。很多人都把功率因数误认为就是cosφ，并用cosφ作为功率因数符号。并以此为基础，得出有功功率P、无功功率Q和视在功率S之间的直角三角形关系。即：

　　P=S*cosφ （1）

　　Q=S*sinφ （2）

　　S2=P2+Q2 （3）

　　功率因数（Power Factor，缩写为PF）表示有功功率与视在功率的比值，常用λ表示，功率因数计算公式如下：

　　λ=P/S

　　视在功率定义为电压有效值U与电流有效值I的乘积，用S表示，基本单位为VA，即S=UI。视在功率也称表观功率。

　　视在功率计算公式如下：

　　S=UI （4）

　　有功功率定义为瞬时功率在一个周期内的积分的平均值，用P表示，基本单位为W，假设交流电周期为T，电压、电流的瞬时值表达式分别为u（t）、i（t），有功功率计算公式如下：

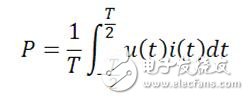　　（5）

　　有功功率也称平均功率。

　　上述视在功率计算公式（4）和有功功率计算公式（5）在任何情况下均能成立。

　　1正弦电路功率因数符号和功率因数计算公式

　　在正弦稳态电路中，根据有功功率计算公式（5），可以推导出下述简化的有功功率计算公式：

　　P=UIcosφ。 （6）

　　φ为正弦电压、电流的相位差。

　　将视在功率计算公式（4）代入正弦电路有功功率计算公式（6），可得到本文开始时提出的式（1）。

　　式（1）只有在正弦稳态电路中才能成立。即：在正弦稳态电路中，功率因数数值上等于位移因数cosφ。由于正弦电路是交流电路的基础，且电网的电压波形为正弦波，早期大部分用电器为线性负载，电流波形也是正弦波。因此，大家习惯了用cosφ作为功率因数符号。

　　非正弦电路功率因数符号和功率因数计算公式

　　随着电力电子技术的发展变频器、整流器等非线性设备得到广泛的应用，非线性设备的特点是，即便采用正弦电压供电，其电流也不是正弦波。另外，电网谐波污染日益严重，电网电压的非正弦性（波形畸变率）日益严重。

　　只要电压和电流两者中有一个或一个以上为非正弦波，式（1）就不再成立，功率因数符号也就不能用cosφ表示。

　　根据傅里叶变换理论，非正弦交流电量可以分解为基波及频率为基波频率整数倍的谐波的线性组合。而有功功率P就等于基波及各次谐波相互作用的有功功率之和。

　　根据三角函数正交性理论，不同频率的正弦波相互作用，不产生有功功率。

　　因此，通用有功功率计算公式（5）可以用下述形式表示：

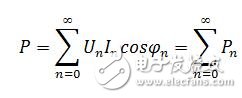　　（7）

　　式中，n=0、1、2.。。

　　U0、I0表示直流分量，U1、I1表示电压、电流基波有效值。P0表示直流功率，P1表示基波有功功率。

　　Un、In表示n次谐波电压和谐波电流的有效值，Pn表示n次谐波电压与n次谐波电流作用下的n次谐波有功功率。

　　φ0=90°，φ1表示基波电压与基波电流的相位差，φn表示n次谐波电压与n次谐波电流的相位差，

　　cosφ1称为基波功率因数或位移因数。

　　类似的，视在功率表示为：

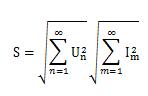　　（8）

　　由有功功率计算公式（7）和视在功率计算公式（8）可得适用非正弦电路的下述功率因数计算公式：

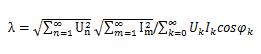　　（9）

　　尽管非正弦电路中，cosφ已经不再等于功率因数，然而，由于长期以来人们习惯了用cosφ作为功率因数符号。因此，在某些特殊的非正弦电路中，功率因数的表达方式仍采用类似的形式表示。

　　特例1：

　　电网供电的非线性设备，对于精度要求不高的场合，可认为电网电压为正弦波。由于是非线性设备，其电流为非正弦波。

　　根据三角函数正交理论，有功功率计算公式如下：

　　P=∑Pn=P1=U1I1cosφ1=UI1cosφ1

　　功率因数计算公式可简化为：

　　λ=P/S=（I1/I）cosφ1 （10）

　　I1/I为电流畸变因数。即功率因数受位移因数和电流畸变因数两部分的影响。

　　特例2：

　　PWM变频器供电的电机的供电电压为非正弦波，电流接近正弦波。对于精度要求不高的场合，可以认为电流为正弦波。

与特例1类似，变频器输出功