LC滤波电路分析，LC滤波电路原理及其时间常数的计算

频率信号的作用。

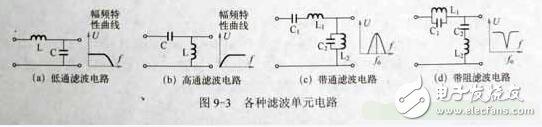
　　以图9—3（a）所示的滤波电路来说，当有信号从左至右传输时，L对低频信号阻碍小，对高频信号阻碍大;C则对低频信号衰减小，对高频信号衰减大。因此该滤波电路容易通过低频信号，称为低通滤波电路。其特点可用图中的幅一频（UF特性f}}I线表示。 对于图9—3（b）所示的滤波电路来说，容易通过高频信号，所以称为高通滤波电路。 对于图9—3（c）所示的滤波电路，它利用C l和L1串联对谐振信号阻抗小、C2和L7并联对谐 振信号阻抗大的特性，能让谐振信号f容易通过，而阻碍其他频率信号通过，所以称为带通滤波电路。该电路的这种特点可用图中的幅一频（U-F特性曲线概括。 对于图9—3（d）所示的滤波电路，它利用Cl和Ll并联对谐振信号阻抗大、C，和L，，串联对谐振信号阻抗小的特点，容易让谐振频率以外的信号通过，而抑制谐振信号厂F通过，所以称为带阻滤波电路。该电路的特点可用图中的幅一频（U-F性曲线来概括。

　　LC滤波电路时间常数的计算：

　　（1）rc振荡回路电容器的电压有：

　　电压=U*exp（-t/rc）

　　U表示电压初值，rc表示电阻电容，t为经过的时间，exp（-t/rc）表示e的-t/rc次方。

　　时间常数τ =rc

　　即电容电阻的乘积，引入时间常数后电压=U*exp（-t/τ）

　　因此，零输入响应的电压变化是一个指数衰减的过程，理论上是无穷时间，但一般是到3~5个时间常数就认为衰减结束了。

　　因此放电时间取决于时间常数τ =rc

　　（2）对于lc振荡回路，情况比较复杂，你只记得于LC的乘积有关就可以了。

　　详细的来说，对一般的LRC回路按

　　R》2*sqr（L/R）

　　R=2*sqr（L/R）

　　R《2*sqr（L/R）

　　sqr（X）表示根号下（X）

　　分为三种情况，大致地说，放电时间取决于电路中R，L，C的值，U不等于0而I=0时，电容通过L，R放电

　　解二阶偏微分方程可以得到两个特征值如：

　　p1=-（R/2L）+spr［（R/2L）*（R/2L）-1/LC］

　　p1=-（R/2L）-spr［（R/2L）*（R/2L）-1/LC］

　　电容电压=［U/（p2-p1）］*［p2exp（p1*t）-p1exp（p2*t）］

　　据此可以分析电容放电时间与LRC的关系.