如何用DFM方法提高LTCC设计效率

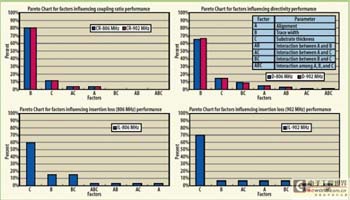
尽管设计人员可以从这些曲线对敏感度做出一些类推，但使用图形表示结果就更容易和更有用。例如排列图(Pareto)显示了某个参数变差对性能影响的百分比。图5给出了对定向耦合器性能变差造成影响的参数或因子的Pareto图。该图显示基底厚度变差对插损的影响超过其它参数或它们的组合。例如，在性能上有60%的变差来自于基底厚度变差的作用。

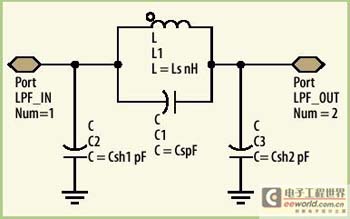
本文中低通滤波器实例采用一个三阶椭圆滤波器设计，使用了一个电感来使插损最小。实际上，滤波器损耗的根本原因来自电感响应或品质因素(Q)。滤波器的全部元件实现为具有内嵌式无源元件的LTCC层。

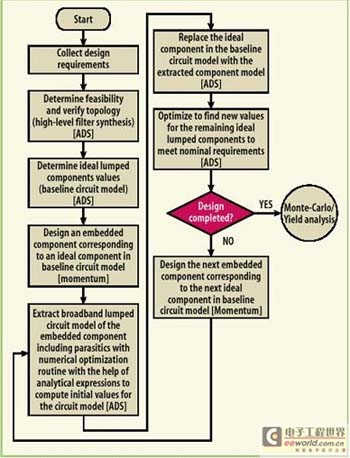
任何设计始于确定性能要求，接下来是可行性研究，这一时期可能设计出电路拓扑结构。对于滤波器，设计人员常常依赖滤波器综合工具来试验不同的结构。这个阶段之后，要确定出基线电路模型及其合适的理想集总元件参数值。由于设计人员必须为LTCC制作一个内嵌式无源部件来代替理想集总元件部件，这就需要进行EM仿真来准确建模和仿真这些内嵌的无源部件。

利用仿真产生的S参数可以抽取出包含寄生电路元件的宽带集总无源模型。抽取过程使用数值优化程序，用解析表达式计算电路模型的各初值。宽带集总无源模型有助于进行统计分析，包括比直接用EM仿真器更为快速实的优化实现。

提取的宽带模型用来代替简单的集总元件模型。然后，用电路仿真器通过对每个元件寻找给定一组性能条件下的最优元件参数值使新的基线电路得到优化。这个过程要反复进行直到所有先前的理想部件被内嵌物理部件所代替。一旦设计满足其性能要求，就该进行蒙特卡洛分析以了解性能作为制造过程的函数的统计特性。

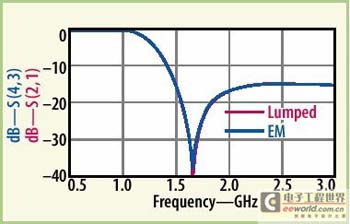
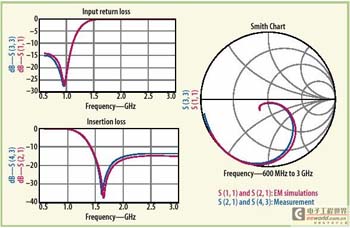
在抽取出宽带模型，获得内嵌电容和电感后，低通滤波器例子的最终布局示于图4。图6针对滤波器插损将EM仿真跟提取的集总部件模型结果进行了比较，集总元件模型与EM模型之间一致性很好。图7把EM仿真响应与测量数据作了对比，结果又一次接近一致。

统计分析(基于蒙特卡洛分析)是采用规定的概率分布，在设计范围内改变一组参数的过程，用来确定性能如何随参数变化而发生改变。这种分析通常用于项目产出，其定义为满足或超过性能期望(指标)项的数量与在统计分析期间分析项总数之比。产出还是给定设计样本达到性能指标的概率。因为将要制造的设计总数会很大或者未知，产出通常是用更小的样本数量或试验次数估计得到，试验数被称作产出估计函数。随着试验次数增加，产出估计就接近真实的设计产出。产出优化使设计性能对于部件变差的敏感度最小化。产出优化估计产出和产出敏感度，并且改变电路统计参数标称值，这是为了同时使统计敏感度最小和电路产出最大。

统计设计流程的第一个步骤是收集厂商的过程变差数据，根据该数据，就能得到用于抽取出的电路模型的统计参数。然后，用这些相关联的统计参数对设计进行统计分析。如果设计满足产出指标，就结束分析过程开始制造过程，否则，就要对抽取的电路模型进行产出优化来修正设计以达到给定的产出指标。用于抽取模型的优化后部件参数值必须被实现成内嵌的无源物理部件。其后，从重设计的内嵌无源物理部件再次抽取出宽带电路模型，并再次进行统计分析直到满足产出指标。LTCC设计过程可以用图8所示的流程图来描述。

对低通滤波器电路实例的6,000次试验进行蒙特卡洛/产出分析(图9)，低通滤波器插损、二阶谐波抑制和三阶谐波抑制的统计分析结果(未给出)表明，这些情形中设计未满足指标，并显示设计通过6000次试验达到100%产出。

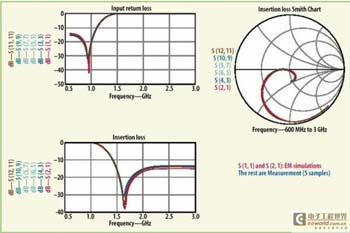
图10给出了总共5个测量样本跟单次EM仿真数据的比较。图中参数S11和S21是EM仿真结果，其它曲线反映测量数据的情况。测量样本数据同仿真结果具有良好的一致性。

两个实例显示DFM提供了获得一次性设计成功的实用手段，甚至在像LTCC具有固有变差那样的过程里。成功依赖于一个经十分慎重选择后得到的设计流程，选用宽带模型尤其重要。在整个设计过程中应用DFM提高了一次性设计成功的机会。尽管这两个说明DFM的例子是基于LTCC，该设计流程同样能用到其它过程。