十种最经典的精密整流电路电路图及其原理,精密整流电路和普通整流电路有什么区别?
十种精密全波整流电路图
图中精密全波整流电路的名称,纯属本人命的名,只是为了区分;除非特殊说明,增益均按1设计。
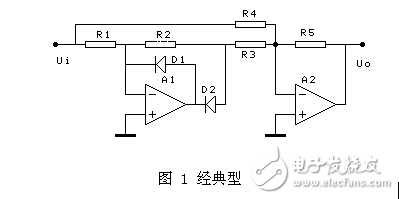
图1是最经典的电路,优点是可以在电阻R5上并联滤波电容。电阻匹配关系为R1=R2,R4=R5=2R3;可以通过更改R5来调节增益。

图2优点是匹配电阻少,只要求R1=R2

图3的优点是输入高阻抗,匹配电阻要求R1=R2,R4=2R3

图4的匹配电阻全部相等,还可以通过改变电阻R1来改变增益。缺点是在输入信号的负半周,A1的负反馈由两路构成,其中一路是R5,另一路是由运放A2复合构成,也有复合运放的缺点。
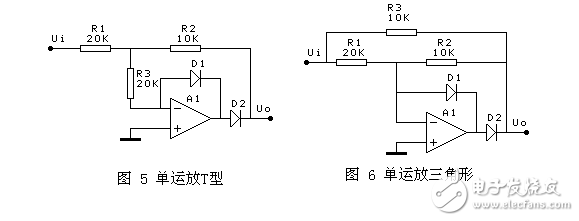
图5 和 图6 要求R1=2R2=2R3,增益为1/2,缺点是:当输入信号正半周时,输出阻抗比较高,可以在输出增加增益为2的同相放大器隔离。另外一个缺点是正半周和负半周的输入阻抗不相等,要求输入信号的内阻忽略不计。
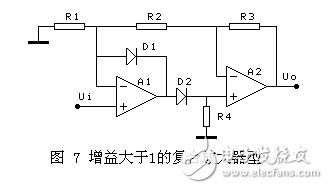
图7正半周,D2通,增益=1+(R2+R3)/R1;负半周增益=-R3/R2;要求正负半周增益的绝对值相等,例如增益取2,可以选R1=30K,R2=10K,R3=20K

图8的电阻匹配关系为R1=R2
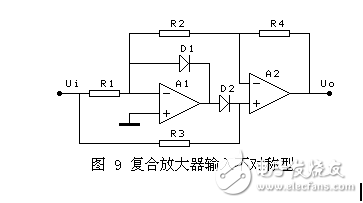
图9要求R1=R2,R4可以用来调节增益,增益等于1+R4/R2;如果R4=0,增益等于1;缺点是正负半波的输入阻抗不相等,要求输入信号的内阻要小,否则输出波形不对称。
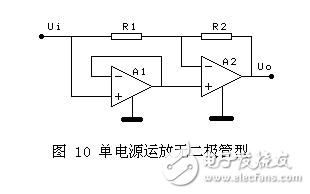
图10是利用单电源运放的跟随器的特性设计的,单电源的跟随器,当输入信号大于0时,输出为跟随器;当输入信号小于0的时候,输出为0.使用时要小心单电源运放在信号很小时的非线性。而且,单电源跟随器在负信号输入时也有非线性。
图7,8,9三种电路,当运放A1输出为正时,A1的负反馈是通过二极管D2和运放A2构成的复合放大器构成的,由于两个运放的复合(乘积)作用,可能环路的增益太高,容易产生振荡。
精密全波电路还有一些没有录入,比如高阻抗型还有一种把A2的同相输入端接到A1的反相输入端的,其实和这个高阻抗型的原理一样,就没有专门收录,其它采用A1的输出只接一个二极管的也没有收录,因为在这个二极管截止时,A1处于开环状态。
精密整流电路和普通整流电路的区别:
将交流电转换为直流电称为整流。全波整流电路的输出保留输入电压的形状,而仅仅改变输入电压的相位。半波和全波整流电路在功能上和精密整流一样,由于二者的适用范围不同,理解时应区分二者的结构和工作原理。
当输入电压为正弦波时,半波整流电路的输出电压波形如图1中uO1所示,全波整流电路的输出电压波形如图1中uO2所示。
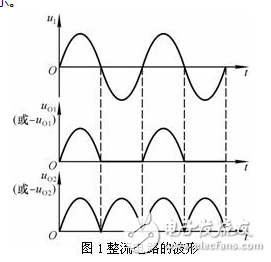
精密整流电路的功能是可以将微弱的交流电压过零处附近准确转换成直流电压。
在图2(a)所示为一般半波整流电路,由于二极管的伏安特性如图(b)所示,当输入电压uI幅值小于二极管的开启电压Uon时,二极管在信号的整个周期均处于截止状态,输出电压始终为零。即使uI幅值足够大,输出电压也只反映uI大于Uon的那部分电压的大小。在uI与Uon相差不大时,输出整流波形在零区附近的失真非常明显。因此,该电路不能对微弱信号整流。
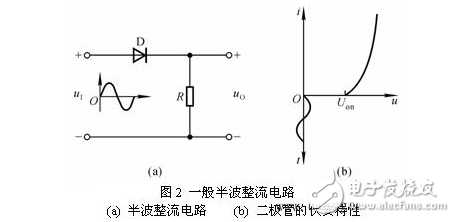
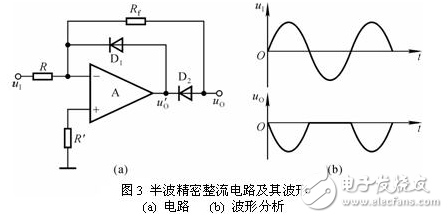
图3(a)所示为半波精密整流电路。当uI>0时,必然使集成运放的输出![]() <0,从而导致二极管D2导通,D1截止,电路实现反相比例运算,输出电压:
<0,从而导致二极管D2导通,D1截止,电路实现反相比例运算,输出电压:
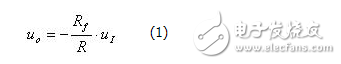
当uI<0时,必然使集成运放的输出![]() >0,从而导致二极管D1导通,D2截止,Rf中电流为零,因此输出电压u0=0。uI和u0的波形如图(b)所示。
>0,从而导致二极管D1导通,D2截止,Rf中电流为零,因此输出电压u0=0。uI和u0的波形如图(b)所示。
如果设二极管的导通电压为0.7V,集成运放的开环差模放大倍数为50万倍,那么为使二极管D1导通,集成运放的净输入电压应为:

同理可估算出为使D2导通,集成运放所需的净输入电压也具有同等数量级。可见,只要输入电压uI使集成运放的净输入电压产生非常微小的变化,就可以改变D1和D2工作状态,从而达到精密整流的目的。
图3(b)所示波形说明当uI>0时u0=-KuI(K>0),当uI<0时u0=0。可以想象,若利用反相求和电路将-KuI与uI负半周波形相加,就可实现全波整流,此处不赘述。
一般整流电路通常用于需要通过整流获得某恒定直流电压的场合,如电子线路的控制电源等。通常在这种应用场合下不需计较整流输出端的波形,而只关心滤波后获得的直流电压的大小。而精密整流常用作信号变换,因而除了相位关系的改变外,主要关心整流输出波形与输入波形的相符程度,任何微小的畸变都会影响精密整流的性能。
- 电动机全波能耗制动控制电路(10-02)
- 多功能逆变电浅谈电力电子技术中的整流电路(10-13)
- 介绍整流电路的类型以及相关原理(05-18)
- 三相桥式全控整流电路原理及电路图,三相桥式全控整流电路原理及电路图(04-02)
- 电容在整流电路中有什么作用?半波整流电路是什么?单相半波可控整流电路的工作原理(04-02)
- 晶闸管整流电路的功率因数是怎么定义的 与哪些因数有关?六个二极管的整流电路画法(04-02)
