数电模电基础知识之搞懂数电技术，你看过保证能熟练运用基础数电技术！

　　一、集成门电路

　　数字集成电路按其内部有源器件的不同可以分为两大类：一类为双极型晶体管集成电路（TTL电路）；另一类为单极型集成电路（MOS管组成的电路）。

　　1．TTL集成逻辑门电路

　　（1）TTL与非门

　　CT74S肖特基系列TTL与非门的电路组成如图2-19（a）所示，它由输入级、中间级、输出级3个部分组成。

　　

　　图2-19 TTL与非门电路图

　　输入级：由多发射极管VT1和电阻R1组成，多发射极管的3个发射结为3个PN结。其作用是对输入变量A、B、C实现逻辑与，所以它相当于一个与门。

　　中间级：由VT2、R2和VT6、RB、RC组成，VT2集电极和发射极同时输出两个逻辑电平相反的信号，用以驱动VT3和VT5。

　　输出级：由VT3、VT4、VT5和R4、R5组成，它采用了达林顿结构，VT3和VT4组成复合管降低了输出高电平时的输出电阻，提高了带负载能力。

　　TTL 与非门的逻辑符号如图 2-19（b）所示；逻辑表达式为：

　　对图2-19所示电路，如果高电平用1表示，低电平用0表示，则可列出图2-19所示的真值表，如表2-1所示。

　　

　　表2-1 TTL与非门真值表

　　（2）集电极开路与非门（OC门）

　　① 工作原理。

　　集电极开路与非门也叫 OC 门，能使门电路输出的电压高于电路的高电平电压值，且门电路的输出端可以并联以实现逻辑与功能，即线与（一般的TTL门电路不能线与）。

　　OC门的电路如图2-20（a）所示，逻辑符号如图2-20（b）所示，逻辑表达式为：

　　

　　图2-20 集电极开路与非门及逻辑符号

　　② OC 门的应用。

　　OC门可以实现线与，如图2-21所示，逻辑表达式为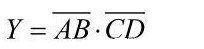；驱动显示器、实现电平转换，如图2-22所示。

　　

　　图2-21 用OC门实现线与

　　（3）与或非门

　　与或非门电路如图2-23（a）所示，逻辑符号如图2-23（b）所示，逻辑表达式为：

　　

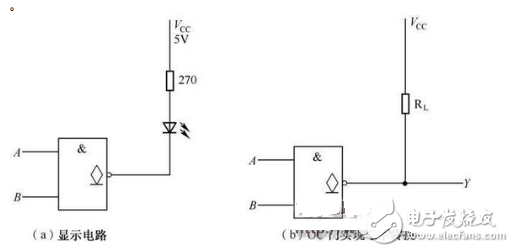
　　图2-22 驱动显示器、实现电平转换

　　

　　图2-23 与或非门及逻辑符号

　　（4）三态输出门

　　三态输出门是指不仅可输出高电平、低电平两个状态，而且还可输出高阻状态的门电路，如图2-24所示，为控制端。

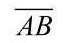　　当=0时，G输出P=1，VD截止，输出Y=，三态门处于工作状态。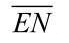低电平有效。

　　

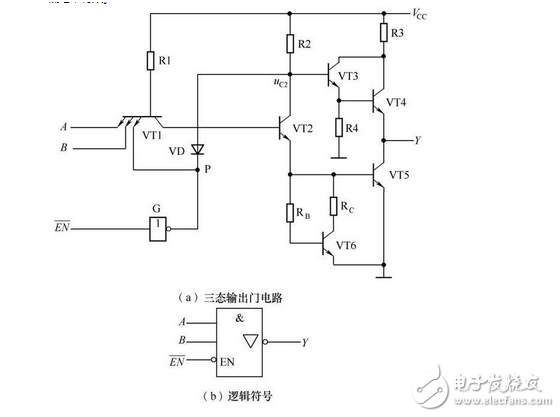
　　图2-24 三态输出与非门及其逻辑符号

　　当=1时，G输出P=0，VD导通，输出高阻状态。

　　2．CMOS集成逻辑门

　　和 TTL 数字集成电路相比，CMOS 电路的突出特点是微功耗、高抗干扰能力。

　　（1）CMOS反相器

　　由两个场效应管组成互补工作状态，如图 2-25 所示。逻辑表达式为：

　　

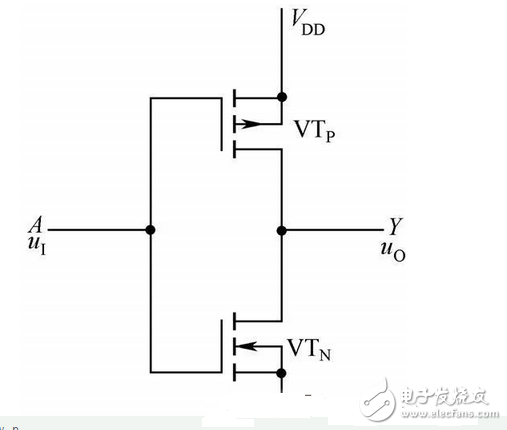
　　图2-25 CMOS 反相器

　　（2）CMOS与非门

　　如图2-26所示，两个串联的增强型NMOS管VTN1和VTN2为驱动管，两个并联的增强型PMOS管VTP1和VTP2为负载管，组成CMOS与非门，逻辑表达式为：。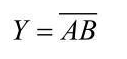

　　（3）CMOS或非门

　　如图2-27所示，两个并联的增强型NMOS管VTN1和VTN2为驱动管，两个串联的增强型PMOS管VTP1和VTP2为负载管，组成CMOS或非门，逻辑表达式为：

　　

　　图2-26 CMOS 与非门

　　

　　图2-27 CMOS 或非门

　　（4）CMOS传输门

　　将两个参数对称一致的增强型NMOS管VTN和PMOS管VTP并联可构成CMOS传输门，电路和逻辑符号如图2-28所示。

　　

　　图2-28 CMOS 传输门及逻辑符号

　　（5）CMOS三态门

　　图 2-29（a）所示为低电平控制的三态门输出，图 2-29（b）为逻辑符号。

　　

　　图2-29 CMOS 三态门输出及逻辑符号

　　当时，VTP2和VTN2导通，VTN1和VTP1组成的CMOS反相器工作，所以。

　　当，VTP2和VTN2同时截止，输出Y对地和对电源VDD都呈高阻状态。

　　（6）CMOS异或门

　　图2-30（a）所示为异或门，图2-30（b）为逻辑符号。

　　

　　图2-30 CMOS 异或门及逻辑符号

　　当输入A=B=0或A=B=1时，即输入信号相同，输出Y=0；当输入A=1或B=1时，即输入信号不同，输出Y=1。其真值表如表2-2所示。

　　

　　表2-2 异或门真值表

　　3．复合门电路

　　除了上述介绍的逻辑门电路外，还有或非门、异或门、同或门等，表2-3是基本门和常用复合门的逻辑符号、逻辑表达式及逻辑功能。

　　表2-3 基本门和常用复合门的对照表

　　二、组合逻辑电路

　　逻辑电路在任何时刻的输出状态只取决于这一时刻的输入状态，而与电路的原来状态无关，则该电路称为组合逻辑电路。

　　1．组合逻辑电路的分析方法

　　（1）分析步骤

　　① 根据给定的逻辑电路写出输出逻辑关系式。一般从输入端向输出端逐级写出各个门输出对其输入的逻辑表达式，从而写出整个逻辑电路的输出对输入变量的逻辑函数式。必要时，可进行化简，求出输出逻辑函数式。

② 列出逻辑函数的真值表。将输入变量的状态以自然二进制数顺序的各种取值组合代入输出逻辑函数式，求出相应的输出状态，并填入表中