基于Zynq的光流法软硬件协同设计与实现

本项目采用的光流算法是基于Horn-Schunck [5]的模型, 与Lucas- Kanade [2]光流算法相比，它算出的光流更稠密，能够精确到每一个像素点；但是它因需要求解欧拉-拉格朗日方程需要成大量的迭代，因此计算光流的时间相当耗时，比如在Zedboard的单核ARM上处理640x480的图片序列需要24.14s才能完成，这表明在传统单架构的嵌入式平台上很难满足光流场实时计算的要求。

1. 基于Horn-Schunck模型的光流算法

1.1 光流的约束条件
光流 15wx鈮?ux, vx, ht)"> 的假设条件认为图像序列,在时间t 15t"> 的某一像素点与在时间 15t+1"> t+1的这一像素点的偏移量 15(x+u,y+v)"> 保持不变，即 。这就是灰度值守恒假设，通过Taylor展开，就能得到光流的约束条件(OFC): ，其中下标表示图像的梯度。

1.2 Horn-Schunck 模型
1981年，Horn和Schunck根据同一个运动物体的光流场具有连续、平滑的特点, 提出一个附加约束条件，将光流场的整体平滑约束转换为一个变分的问题。它的能量方程如下：
其中数据项表示灰度值守恒约束，平滑项表示光流平滑约束。

1.3 Euler-Lagrange方程
根据Horn-Schunck能量方程，可以推导出离散的欧拉-拉格朗日方程如下：

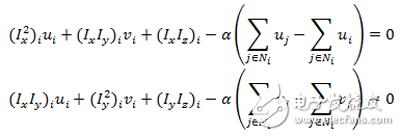
其中， 表示图像像素点的坐标， 表示一个像素点的上下左右四个方向的相邻的像素点，当然，在图像的边界会少于四个元素。

1.4 超松弛迭代 （SOR）
根据上面的欧拉-拉格朗日方程，不难推到出迭代方程。这里选用收敛速度最快的超松弛算法（SOR），光流的初始值是，迭代方程如下：

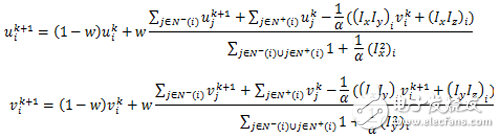
其中， w是迭代的权重因子, k 是迭代的次数， 是光流的计算的权值， 表示第 个像素点的上和左的相邻像素点，表示第 个像素点的下和右的相邻像素点。

2 工作流程介绍

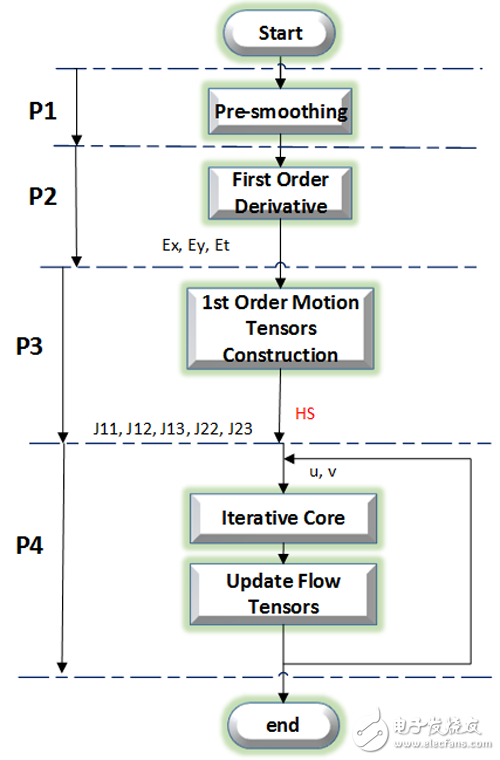
根据上面的理论分析，可以把光流法的计算划分为四个阶段：预处理阶段（P1）、梯度计算阶段（P2）、运动模型构造阶段（P3）和迭代阶段（P5），如图2所示。

2.1 预处理阶段（P1）
这一阶段是平滑处理的图像序列，它的作用是用来减少图像噪音和外部的影响，通常用卷积来实现的。这一阶段是一个通用的图像操作。

2.2 梯度计算阶段（P2）
这一阶段是用来计算平滑好的图像的梯度，包括水平梯度、垂直梯度和时间梯度。计算梯度通常也是通过卷积来实现的。

2.3 运动模型构造阶段（P3）
这一阶段是根据计算出来的梯度来构造运动模型的信息。根据超松弛公式可以推出需要构造五个运动模型的信息，即J11、J12、J13、J22、J23。它的操作就是矩阵乘法。

2.4 迭代阶段（P4）
这一阶段就是通过超松弛算法计算光流的结果，每一次迭代完了需要把光流的信息更新一遍，再作为初始值进行下一次迭代。这一阶段的操作是根据迭代公式来实现的。

2.3 软件的执行时间

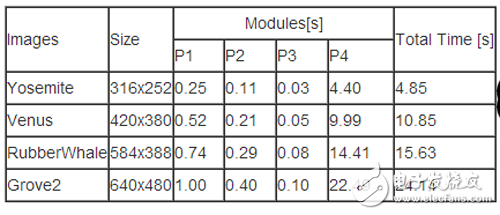
软件的实验平台是在Zedboard上ARM Cortex-A9处理器上来测试的，其中包括2个32KB 一级缓存和512KB的共享二级缓存，以及512MB的内存空间，采用的测试集下载自 。Horn-Schunck光流算法是通过ANSI C实现的。其中迭代的次数设为100次。

基于Horn-Schunck模型的稠密光流法在软件上的执行时间如表1所示，不难发现，随着图像的不断变大，所需要的执行时间不断增大；其中迭代部分（P4）占到很大的时间比例。