MEMS惯性测量单元（IMU）/陀螺仪对准基础

应用制定精度标准时，了解对准误差与其对陀螺仪精度影响之间的基本关系是一个很好的着手点。为了说明该过程，图5提供了三轴陀螺仪系统的通用模型。图中的三条绿色实线代表全局坐标系的三轴，黑色实线代表所有三个陀螺仪的旋转轴，带Ψ标签代表全局坐标系与陀螺仪轴之间的对准误差。公式5、公式6和公式7显示了对准误差对各陀螺仪绕全局坐标系中指定轴旋转的响应的影响。在这些公式中，对准角度误差的余弦引入一个比例误差。

　　图5：正交三轴陀螺仪的对准误差。

　　对准误差还会对各轴产生跨轴影响。为了量化这些影响，需要将各轴的对准角度误差分解为与其它两轴相关的两个分量。例如，ΨX有一个y轴分量（φXY）和一个z轴分量（φXZ），导致x轴陀螺仪对绕全局坐标系中所有三轴旋转（ωX， ωY， ωZ）的响应扩展如下：

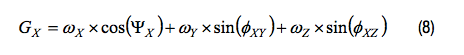
　　y轴和z轴陀螺仪也有同样的扩展：

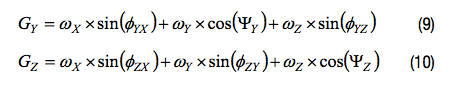
　　对公式8、公式9和公式10的两侧积分，可得到关于角位移的类似关系。在得到的公式11、公式12和公式13中，我们关心的角度是相对于全局坐标系的角位移（θXω， θYω， θZω）和各陀螺仪的积分（θXG， θYG， θZG）。

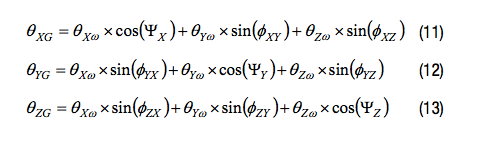
　　示例2

　　一种地面无人驾驶车辆（UV）利用MEMS IMU作为平台稳定控制（PSC）系统中的反馈传感器以支持其天线。此系统采用RSS调谐器环路，后者要求方位角和仰角保持在±1？范围内，以便维持连续通信。在大多数动态情况下，PSC高度依赖y轴陀螺仪测量来控制仰角，以及依赖z轴陀螺仪测量来控制方位角。在此类动态情况下，航向角（θZω）的最大变化为30？，并且在作这种机动期间没有绕x轴或y轴的旋转（θXω = θYω = 0）。

　　求解

　　由于绕x轴和y轴的旋转为0，公式8和公式9可简化为：

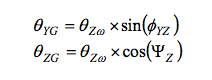
　　从y轴开始，设θYG的最大边界为1？，求解对准误差项ΦYZ。这样便可求得y轴陀螺仪的最大允许对准误差为1.9度。

　　对于z轴，设θZω等于30？，θZG和θZω之差的最大边界为1度，然后求解ΨZ。这样便可求得z轴陀螺仪的最大允许对准误差为14.8度。

　　上述计算表明，对于这种特定机动/情形，y轴和z轴之间的跨轴行为要求对准精度约为1.9度。

　　电子对准 

　　在IMU和安装系统不满足关键系统目标的情况下，电子对准提供了一种减小对准误差的方法。该过程有两个重要步骤：测定对准误差项（IMU安装之后）和制定一个校正对准矩阵。将该矩阵应用于陀螺仪阵列时，陀螺仪将像已与全局坐标系对准一样作出响应。公式14为此过程提供了一个系统模型，其中绕全局坐标系各轴的旋转（ω）是三个系统输入，三个陀螺仪响应（G）是系统输出，3 &TImes; 3矩阵（M）代表输入与输出之间的系统行为（包括对准误差）。

　　通过简单的算术操作可得，陀螺仪测量结果（G）与M的逆矩阵（M–1）的乘积等于全局坐标系的旋转阵列（ω）。因此，对准矩阵等于M–1。

　　基于公式8、公式9和公式10，可将公式14扩展以包括对准误差项，如公式16所示，公式17和公式18是更一般形式：

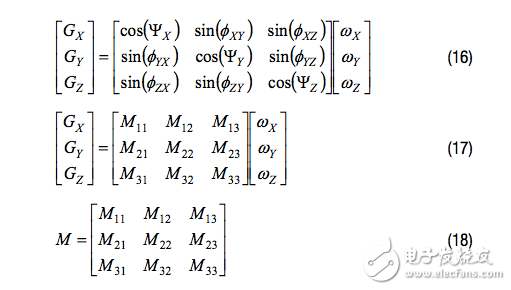
　　一次仅绕一个轴旋转整个系统可将系统模型简化到足够简单的程度，使得矩阵中的每个元素都可以通过一次陀螺仪测量获得。例如，让系统绕x轴旋转（ωX = ωTR， ωY = 0， ωZ = 0），同时观测所有三个轴，则M11、M21和M31的关系可简化如下：

　　采用同样的方法，绕y轴旋转（ωX = 0， ωY = ωTR， ωZ = 0），则M12、M22和M32的关系可简化如下：

　　最后，绕z轴旋转（ωX = 0， ωY = 0， ωZ = ωTR），则M13、M23和M33的关系可简化如下：

　　显然，运动配置（ω）的精度和陀螺仪测量（G）对此过程有直接影响。具体说来，偏轴运动对此过程有显著影响，当购买和部署依赖这些要求的惯性测试设备时，必须予以考虑。就陀螺仪精度而言，偏置和噪声是两大威胁，在此过程中通常需要考虑。为了管控陀螺仪测量中残余偏置误差（bE）的影响，有一个技巧是使用两个不同的旋转速率——大小相等但方向相反。例如，绕y轴沿正方向旋转时（ωY = ωTR， ωX = ωZ = 0），公式28描述了z轴陀螺仪响应和偏置误差。公式29则描述了绕y轴沿负方向旋转时（ωY = –ωTR， ωX = ωZ = 0）z轴陀螺仪的响应。

变换公式29，写出偏置误差（bE）的表示形式，代入公式2