基于STM32的智能参数测试仪的设计方案

电阻子程序、触点电阻子程序、吸合/ 释放电压子程序、吸合/ 释放时间子程序。

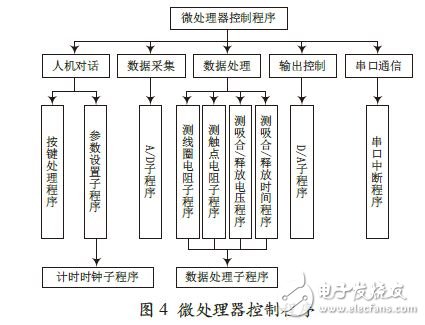
　　3.2 吸合电压算法设计

　　对于吸合/ 释放电压的测试，这里将对比三种测试算法：

　　二分算法、步进自适应中值算法和差异比较算法［8］。

　　3.2.1 二分算法

　　函数f（x），对于一个实数a，当x=a 时，若f（a）=0，则把x=a 叫做函数f（x） 的零点。设f（x） 在区间（X，Y） 上连续，a、b 属于区间（x，y），且f（a），f（b） 异号，则在区间（a，b） 内一定存在至少一个零点，然后求f［（a+b）/2］。假定a《b，f（a）《0，f（b）》0，那么：

　　如果f［（a+b）/2］=0，则x=（a+b）/2 就是零点。

　　如果f［（a+b）/2］《0，说明区间（（a+b）/2，b） 内有零点，再次对新区间（（a+b）/2，b） 取中值代入函数，进行中点函数值判断。

　　如果f［（a+b）/2］》0，说明区间（a，（a+b）/2） 内有零点，再次对新区间（a，（a+b）/2） 取中值代入函数，进行中点函数值判断。

　　通过以上反复的区间取值，可以把f（x） 的零点所在小区间收缩一半，使区间的两个端点逐步迫近函数的零点，最终以求得零点的近似值。

　　这就是二分算法的基本原理。

　　3.2.2 步进自适应中值算法

　　同简单二分算法一样，确定A、B 两个电压值，其中A 无法使触点吸合，B 保证发生触点吸合。然后求得A、B 的平均值C，如果C 小于触点的阈值电压，则在B 电压量的基础上步进式地减小一定幅度的电压X，得到电压量D ;如果C 大于触点的触发电压，那么在A 电压量的基础上，步进式地增加一定幅度的电压X［9］，然后重复以上步骤。如果发生某一步进增加时，触点发生吸合，则继电器的吸合电压介于触点触发的前后两个电压平均数值之间。

　　3.2.3 差异比较算法

　　差异比较算法是通过比较输入值和输出值的大小，将发生差异型变化的数值进行筛选并记录。选择这个算法主要是针对二次发生的吸合释放过程。

　　三种算法中，二分算法有可能让程序进入死循环，差异比较算法相对前两者速度较慢，所以本系统最终采用步进自适应中值算法。

　　3.3 上位机程序设计

　　本系统的上位机界面程序采用C++ 程序编写，它主要包括参数设置区域、参数显示区域、继电器类型选择和控制按键等几部分。参数设置区域是完成对所测继电器的相关参数上下限参数的设置，比如吸合电压上下限的设置。参数显示区域是显示所测参数大小的，这里还包括了一个参数选择复选框，如果选上则表示需要对此参数进行检测，如果不选则系统不对此部分参数进行检测。图5 所示为其上位机界面。

　　3.4 实验结果

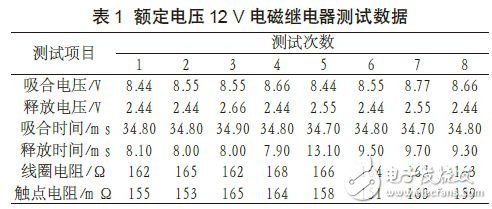
　　在调试好的样机上分别可对吸合电压等六个参数进行测试，为了减少一次测试数据的偶然性，每个参数均测试了八组数据进行处理，实验结果如表1 所示。从表1 中的数据可以发现，其测试数据变化范围小，系统性能较稳定，总体性能能够令人满意。

　　4 结语

　　本文是结合前人的研究成果基础上而提出的一种基于STM32 的智能参数测试仪的设计方案，该方案中所设计的测试仪由STM32 作为主控芯片，并结合先进的电子测量线路来对继电器的主要电气参数进行测量。实验结果表明，本系统测试结果准确性高，工作稳定，总体性能令人满意。