有源滤波器中的相位关系
减器组成的反馈网络来提高。不过,改变增益将影响到决定频率网络的表达式,而且需要重新计算元件的值。该放大器的动态特性也需要更严格的考察,因为它们在环路中引入了增益。
多路反馈(Multiple-Feedback,MFB)低通滤波器
多路反馈滤波器是一种单放大器电路结构,反馈环路是基于运放的积分器(反相配置),如图12所示。因此,运放参数对传递函数之间的影响要大于Sallen-Key的实现方案。要产生一个高Q、高频电路是很困难的,因为运放在高频段的开环增益有限。一条指导方针是,运放的开环增益应该至少比谐振(或者截止)频率处的幅值响应高出20dB(即10倍于之),包括滤波器的Q值造成的峰值。由于Q值而造成的尖峰将具有如下的幅值
| (5) |
式中:H是电路的增益。
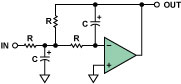
图12. 2极点、多路反馈(MFB)、低通滤波器
该多路反馈滤波器会使信号反相。这等价于让滤波器自身的相移增加了180°。图4示出了相位-频率变化关系(右轴)。这将被称为反相、二阶、低通响应。值得注意的是,在得到给定响应特性的条件下,多路反馈结构中的最大和最小元件值之间的差异要大于Sallen-Key实现方案中的。
多路反馈(MFB)、高通滤波器
上面关于多路反馈、低通滤波器的评述也适用于高通的情形。图13示出一个多路反馈、高通滤波器的原理图,其理想的相移-滤波特性则示于图5中(右轴)。这被称为反相、二阶、高通响应特性。
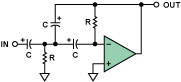
图13. 2极点、多路反馈(MFB)高通滤波器
要保证这种滤波器的具体电路实现在高频情况下的稳定性是十分困难的,因为它是在一个微分器的基础上构建的,与所有的微分器电路所类似的是,它在更高的频率上闭环增益更大,因此会对噪声产生放大作用。
状态变量型滤波器
图14示出了一种状态变量实现方案。该结构是最灵活和最精确的实现方案,付出的代价是电路元件的数量大大增加,其中包括了3个运放。所有3个主要的参数(增益、Q和ω0)都可以独立调节,而且可以同时提供低通、高通和带通输出。该滤波器的增益也是独立的变量。
由于状态变量滤波器的所有参数都可以独立调节,故其元件值的散布变得很小。而且由于温度和元件公差所带来的失配也可以最小化。与上面的多路反馈电路类似的是,积分器部分所使用的运放的增益带宽积也成为电路的限制条件。
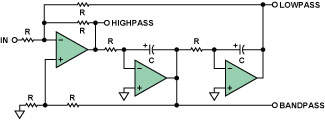
图14. 2极点、状态变量滤波器
其中低通滤波段的相移-频率特性属于一个反相的二阶型响应(参见图4,右轴),高通段电路将具有反相高通响应(参见图5,右轴)。
双二阶(biquad)
状态变量滤波器的一个近亲是双二阶型(参见图15)。该电路的名称最早是由J. Tow于1968年使用的(见参考文献6),后来由L.C. Thomas 于1971年使用(见文献5),其工作是基于如下的事实:传递函数是两个二阶项之比。该电路与状态变量电路之间存在轻微的区别。在这一结构中,不能提供单独的高通输出。不过它具有两路低通输出,其中一路是同相的(LOWPASS1),另一路是反相的(LOWPASS2)。
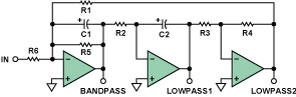
图15. 标准的双二阶2极点电路
由于添加了第四个放大器电路,故可以实现高通、陷波(低通、标准和高通)以及全通型滤波器。图16示出一个带有高通电路的双二阶电路的原理图。
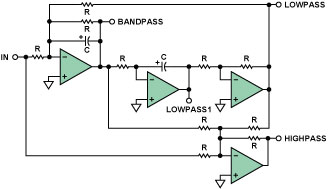
图16. 2极点双二阶滤波器(带有高通段)
其中LOWPASS1段的相移-频率特性属于同相、二阶、低通型响应(参见图4的左轴)。LOWPASS2段将具有反相的二阶型响应(参见图4,右轴)。HIGHPASS段的相移特性属于反相特性(参见图5,右轴)。
结论
我们已经看到用于构建一个滤波器的拓扑将影响其实际的相位响应。这会是确定所用的拓扑时需要考虑的一个因素。表1对本文中讨论的各种低通滤波器结构的相移范围进行了比较。
表1. 低通滤波器架构的相移范围
低通滤波器 | ||
| 滤波器拓扑结构 | 单相 | 相位变化范围 |
| 单极点,无源 | 同相 | 0° to –90° |
| 单极点,有源 | 反相 | 180° to 90° |
| 2极点,Sallen-Key | 同相 | 0° to –180° |
| 2极点,多路反馈 | 反相 | 180° to 0° |
| 2极点,状态变量 | 反相 | 180° to 0° |
| 2极点双二阶低通1 | 同相 | 0° to –180° |
| 2极点双二阶低通2 | 反相 | 180° to 0° |
类似的,表2对各种高通滤波器结构进行了比较。
表2. 高通滤波器拓扑相移范围
高通滤波器 | ||
| 滤波器拓扑结构 | 单相 | 相位变化范围 |
| 单极点,无源 | 同相 | –90° to 0° |
| 单极点,有源 | 反相 | –90° to –180° |
| 2极点,Sallen-Key | 同相 | 180° to 0° |
| 2极点,多路反馈 | 反相 | 0° to –180° |
| 2极点,状态变量 | 反相 | 0° to –180° |
| 2极点双二阶 | 反相 | 0° to –180° |
相移特性随Q的变化特性
上述的2阶响应的Q值都是0.707。图17示出了Q的变化对低通滤波器的相位响应的影响(对高通滤波器的影响也类似)。图中绘出了Q = 0.1,0.5,0.707,1,2,5,10和20时的相位响应曲线。值得注意的是,Q值较低的情况下,在远低于截止频率的频率上相位就开始发生变化。
