MEMS振动监控系统设计简介

持续监控特定频带，通过附近的控制面板提供报警灯和关键灯信号。 制造商在机械设计方面的知识有助于带通滤波器的设计，尤其是在启动频率、停机频率和带通滚降速率方面。 旋转速度、机械结构的自然频率、因故障而异的振动都可能影响带通滤波器。 尽管这种方法非常简单，但当有特定机器的历史数据时，振动监控要求也可能发生变化。 监控要求的变化可能导致滤波器结构的变化，从而可能造成重复的工程成本。 开发人员可以通过数字化传感器响应，实现关键信号处理功能（如滤波、rms计算和电平检测器），利用辅助I/O输出控制指示器灯的方式，以复杂性换取灵活性，或提供数字输出。

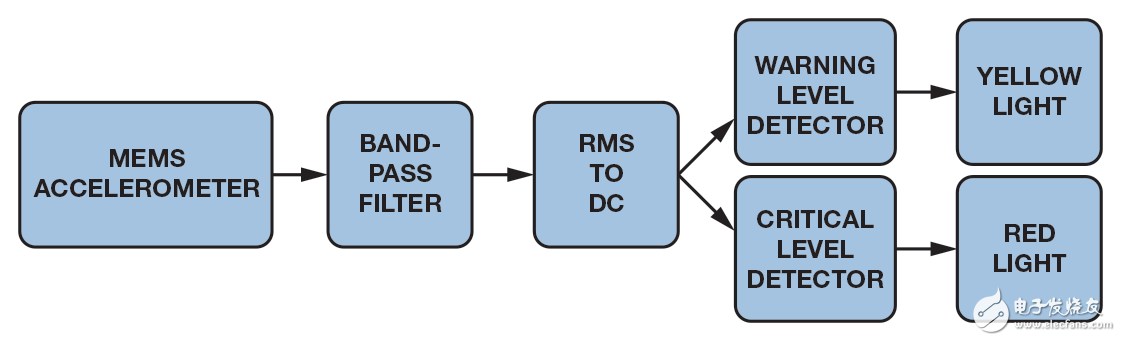
　　图3. 时域振动信号链示例

　　图4所示为ADIS16228的信号链ADIS16228采用一个带FFT分析和存储功能的数字三轴振动传感器监控设备振动的频谱成分。

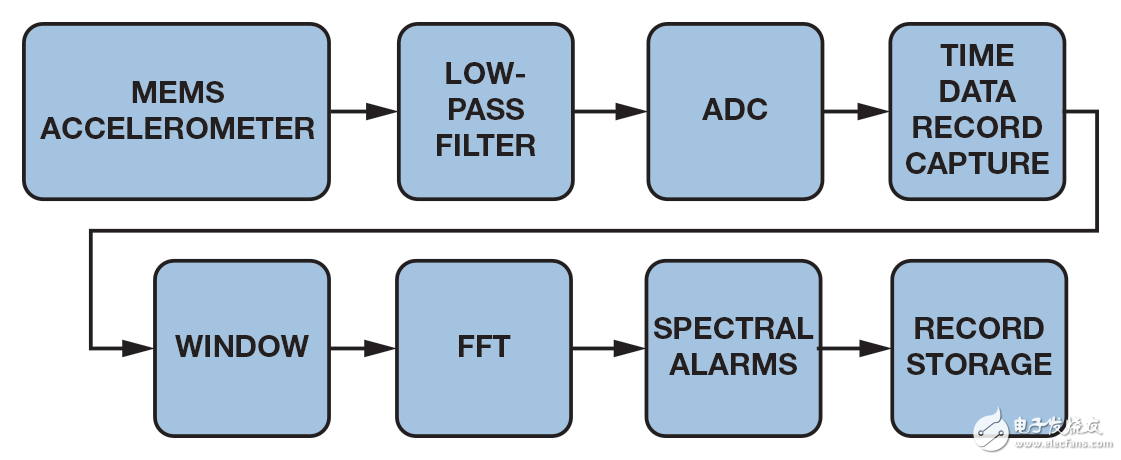
　　图4. 用于频谱振动分析的ADIS16228信号链

　　内核传感器

　　两种方式的内核传感器都可以是MEMS加速度计。 选择内核传感器时，最重要的属性为轴数、封装/装配要求、电气接口（模拟/数字）、频率响应（带宽）、测量范围、噪声和线性度。 尽管许多三轴MEMS加速度计都支持直接连接多数嵌入式处理器，但要获得最高性能则可能要求采用具有模拟输出的单轴或双轴解决方案。 例如，ADXL001高性能宽带iMEMS®加速度计就利用22-kHz谐振提供最宽的带宽，但它只是一款单轴模拟输出器件。 在配有模数转换通道的系统中，模拟输出可实现快速接口，但当前的开发趋势似乎更青睐于那些搭载了数字接口的传感器。

　　内核传感器的频率响应和测量范围决定其输出饱和前可以支持的最大振动频率和幅度。 饱和会降低频谱响应，从而产生可能导致故障报警的杂散成分，即使饱和频率不影响目标频率时也是如此。

　　频率响应和测量范围限制着传感器的响应，其噪声和线性度则限制着分辨率。 噪声决定将在输出中响应的振动下限，而线性度则决定振动信号产生的故障谐波量。

　　模拟滤波器

　　模拟滤波器将信号成分限制在一个奈奎斯特区之内，即为示例系统采样速率的一半。 即使滤波器截止频率处于奈奎斯特区之内，也不可能无限制地抵制高频组分，这些高频组分仍可能折回通带中。 对于只监控第一奈奎斯特区的系统，这种折回行为可能产生假故障，并扭曲特定频率下的振动成分。

　　在振动检测应用中，时间相干采样往往并不实用，因为时间记录起始和结束处的非零采样值会导致较大的频谱泄漏，从而可能降低FFT分辨率。 在计算FFT前应用窗口函数有助于控制频谱泄漏。 最佳窗口函数取决于实际信号，但通常需要衡量的因素包括过程损失、频谱泄漏、旁瓣位置和旁瓣电平。

　　快速傅里叶变换（FFT）

　　FFT是分析离散时间数据的一种高效算法。 该过程将时间记录转换为离散频谱记录，其中，每个采样代表奈奎斯特区的一个离散频段。 输出采样的总数等于原始时间记录中的采样数，在大多数情况下，为二项级数中的一个数字（1、2、4、8……）。 频谱数据同时包括幅度和相位信息，可采用矩形或极性格式表示。 采用矩形表示时，FFT仓的一半含有模值信息，另一半则含有相位信息。 采用极性表示时，FFT仓的一半含有实部结果，另一半则含有虚部结果。

　　在某些情况下，幅度和相位信息都有用，但幅度/频率关系含有的信息往往足以检测关键变化。 对于只提供幅度结果的器件，FFT谱线的数量等于原始时域记录中采样数的一半。 FFT频谱宽度等于采样速率除以记录总数。 在一定程度上，每个FFT频谱都像是时域中一个独立的带通滤波器。 图5为MEMS振动传感器的一个实际示例，其中，采样速率为20480 SPS，始于512点记录。 在这种情况下，传感器只提供幅度信息，因此，总数为256，频谱宽度等于40 Hz （20480/512）。

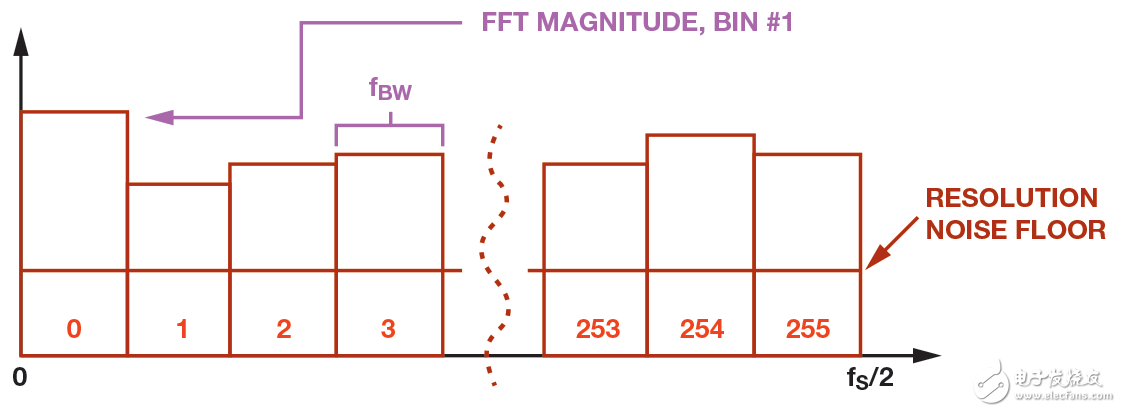
　　图5. ADIS16228 FFT输出

　　频谱宽度非常重要，因为当频率从一个谱线转换到一个邻近谱线时，频谱宽度决定频率分辨率，同时还决定包含的总噪声。 总噪声（rms）等于噪声密度（~240 μg/√Hz） 与频谱宽度平方根（√40 Hz）之积，约合1.5 mg rms。 对于噪声对振动分辨影响最大的低频应用，可在FFT过程之前采用一个抽取滤波器，这样可以提高频率和幅度分辨率，而无需更改ADC的采样频率。 以256对20480 SPS的采样速率进行抽取计算，可使频率分辨率增强256倍，同时使噪声降低16倍。

　　频谱报警

使用FFT的一个关键优势是可以简化频谱报警的应用。 图6中的示例包括5个独立的频谱报警，分别负责监控机器自然频率（#1）、谐波（#2、#3和#4）以及宽带成分（#5）。 报警和临界电平对