语音处理检测技术端点检测、降噪和压缩详解

使用循环神经网络（Recurrent Neural Networks， RNN）技术来进行语音的端点检测，实际的效果可以关注讯飞的产品。

　　▎降噪

　　降噪又称噪声抑制（Noise Reduction），前文提到，实际采集到的音频通常会有一定强度的背景音，这些背景音一般是背景噪音，当背景噪音强度较大时，会对语音应用的效果产生明显的影响，比如语音识别率降低，端点检测灵敏度下降等，因此，在语音的前端处理中，进行噪声抑制是很有必要的。

　　噪声有很多种，既有频谱稳定的白噪声，又有不稳定的脉冲噪声和起伏噪声，在语音应用中，稳定的背景噪音最为常见，技术也最成熟，效果也最好。本课程只讨论稳定的白噪声，即总是假设背景噪声的频谱是稳定或者是准稳定的。

　　前面讲的语音端点检测是在时域上进行的，降噪的过程则是在频域上进行的，为此，我们先来简单介绍或者说复习一下用于时域-频域相互转换的重要工具——傅里叶变换。

　　为了更容易理解，先看高等数学中学过的傅里叶级数，高等数学理论指出，一个满足Dirichlet条件的周期为2T的函数f（t），可以展开成傅里叶级数：

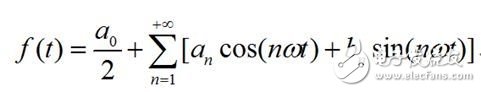
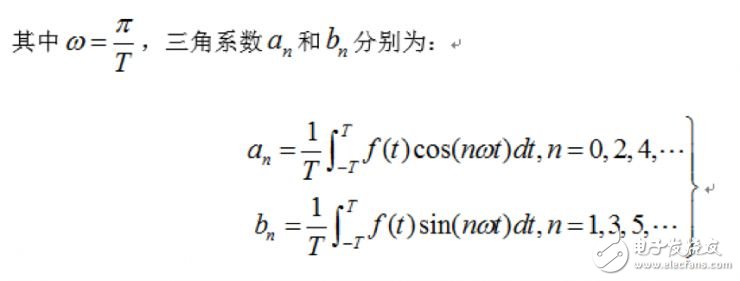
　　对于一般的连续时域信号f（t），设其定义域为［0，T］，对其进行奇延拓后，其傅里叶级数如下式：

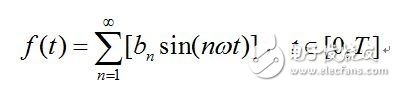
　　bn的计算同上，由上式可知，任何一个连续的时域信号f（t），都可以由一组三角函数线性叠加而成。或者说， f（t）都可以由一个三角函数线性组合组成的序列来无限的逼近。信号的傅里叶级数展示的是构成信号的频率以及各个频率处的振幅，因此，式子的右端又可以看做是信号f（t）的频谱，说的更直白一点，信号的频谱就是指这个信号有哪些频率成分，各个频率的振幅如何。上式从左到右的过程是一个求已知信号的频谱的过程，从右到左的过程是一个由信号的频谱重构该信号的过程。

　　虽然由信号的傅里叶级数很容易理解频谱的概念，但在实际中求取信号的频谱时，使用的是傅里叶级数的一种推广形式——傅里叶变换。

　　傅里叶变换是一个大的家族，在不同的应用领域，有不同的形式，在这里我们只给出两种形式——连续形式的傅里叶变换和离散傅里叶变换：

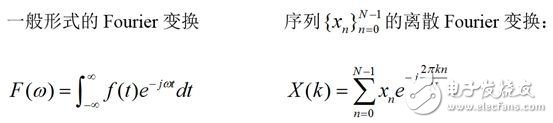
　　其中的j是虚数单位，也就是j*j=-1，其对应的傅里叶逆变换分别为：

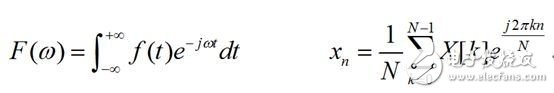
　　在实际应用中，将数字采样信号进行傅里叶变换后，可以得到信号的频谱。频域上的处理完成后，可以使用傅里叶逆变换将信号由频域转换到时域中。对，傅里叶变换是一个可以完成由时域向频域转换的重要工具，一个信号经傅里叶变换后，可以得到信号的频谱。

　　以上是傅里叶变换的简单介绍，数学功底不太好的朋友看不大懂也没关系，只要明白，一个时域信号进行傅里叶变换后，可以得到这个信号的频谱，即完成如下转换：

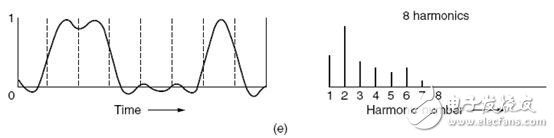
　　左面的是时域信号，右面的是对应的频谱，时域信号一般关注的是什么时间取什么值，频域信号关心的是频率分布和振幅。

　　有了以上的理论作为基础，理解降噪的原理就容易多了，噪音抑制的关键是提取出噪声的频谱，然后将含噪语音根据噪声的频谱做一个反向的补偿运算，从而得到降噪后的语音。这句话很重要，后面的内容都是围绕这句话展开的。

　　噪声抑制的一般流程如下图所示：

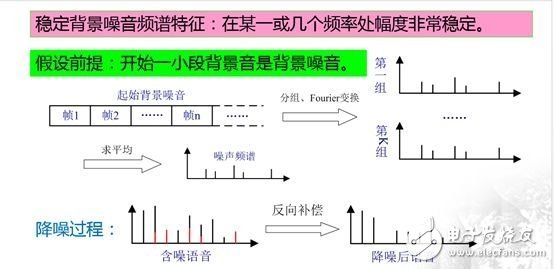
　　同端点检测类似，假设音频起始处的一小段语音是背景音，这一假设非常重要，因为这一小段背景音也是背景噪声，是提取噪声频谱的基础。

　　降噪过程：首先将这一小段背景音进行分帧，并按照帧的先后顺序进行分组，每组的帧数可以为10或其他值，组的数量一般不少于5，随后对每组背景噪声数据帧使用傅里叶变换得到其频谱，再将各频谱求平均后得到背景噪声的频谱。

　　得到噪声的频谱后，降噪的过程就非常简单了，上图下面左侧的图中红色部分即为噪声的频谱，黑色的线为有效语音信号的频谱，两者共同构成含噪语音的频谱，用含噪语音的频谱减去噪音频谱后得到降噪后语音的频谱，再使用傅里叶逆变换转回到时域中，从而得到降噪后的语音数据。

　　下图展示了降噪的效果

　　左右两幅图是降噪前后时域中的对比，左面的是含噪语音信号，从图中可以看到噪声还是很明显的。右侧的是降噪后的语音信号，可以看出，背景噪声被大大的抑制了。

　　下面两幅图是频域中的对比

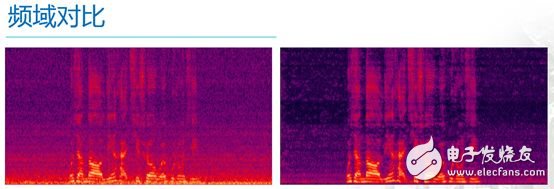
其中横轴表示时间轴，纵轴表示频率，左面的是含噪语音，其中的亮红色部分是有效语音，而那些像沙子一样的紫色的部分则是噪声。从图中可以看出，噪声不仅是"无时不在"，而且还是"无处不在"，也就是在各种频率处都有分布，右侧的是降噪后的语音，可以很明显的看出，降噪前那些像沙子一样的紫色的