GMM-HMM语音识别原理详解

，即，x属于第j个高斯的概率。怎么求捏？

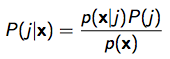
　　fig8. bayesian formula of P（ j | x ）

　　根据上图 P（j | x）， 我们需要求P（x|j）和P（j）去估计P（j|x）。

　　这里由于P（x|j）和P（j）都不知道，需要用EM算法迭代估计以最大化P（x） = P（x1）*p（x2）*.。.*P（xn）：

　　A. 初始化（可以用kmeans）得到P（j）

　　B. 迭代

　　E（estimate）-step： 根据当前参数 （means， variances， mixing parameters）估计P（j|x）

　　M（maximization）-step： 根据当前P（j|x） 计算GMM参数（根据fig4 下面的公式：）

　　
 其中

　　②Training the params of HMM

　　前面已经有了GMM的training过程。在这一步，我们的目标是：从observation序列中估计HMM参数λ；

　　假设状态->observation服从单核高斯概率分布：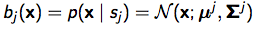
　　则λ由两部分组成：

　　HMM训练过程：迭代

　　E（estimate）-step： 给定observation序列，估计时刻t处于状态sj的概率

　　M（maximization）-step： 根据重新估计HMM参数aij.

　　其中，

　　E-step： 给定observation序列，估计时刻t处于状态sj的概率

　　为了估计， 定义： t时刻处于状态sj的话，t时刻未来observation的概率。即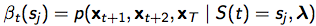

　　这个可以递归计算：β_t（si）=从状态 si 转移到其他状态 sj 的概率aij * 状态 i 下观测到x_{t+1}的概率bi（x_{t+1}） * t时刻处于状态sj的话{t+1}后observation概率β_{t+1}（sj）

　　即：

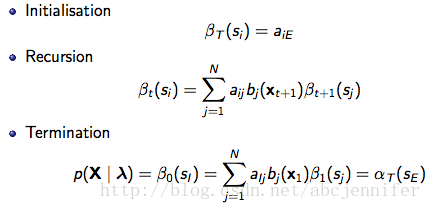
　　定义刚才的为state occupation probability，表示给定observation序列，时刻t处于状态sj的概率P（S（t）=sj | X，λ） 。根据贝叶斯公式p（A|B，C） = P（A，B|C）/P（B|C），有：

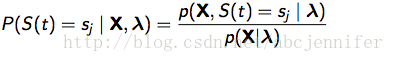
　　由于分子p（A，B|C）为

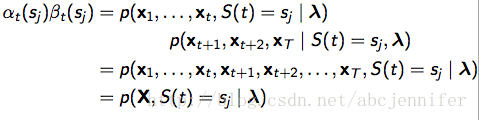
　　其中，αt（sj）表示HMM在时刻t处于状态j，且observation = {x1，。。.，xt}的概率；

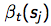　　： t时刻处于状态sj的话，t时刻未来observation的概率；

　　且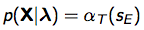

　　finally， 带入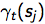的定义式有：

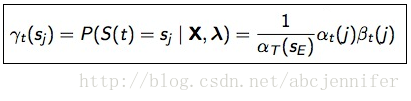
　　好，终于搞定！对应上面的E-step目标，只要给定了observation和当前HMM参数 λ，我们就可以估计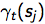了对吧 （*^__^*）

　　M-step：根据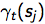重新估计HMM参数λ：

　　对于λ中高斯参数部分，和GMM的M-step是一样一样的（只不过这里写成向量形式）：

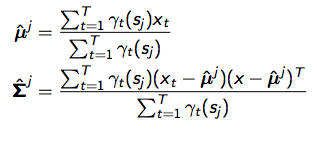
　　对于λ中的状态转移概率aij， 定义C（Si->Sj）为从状态Si转到Sj的次数，有

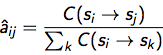
　　实际计算时，定义每一时刻的转移概率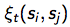为时刻t从si->sj的概率：

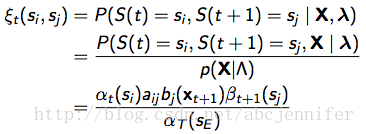
　　那么就有：

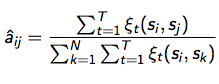
　　把HMM的EM迭代过程和要求的参数写专业点，就是这样的：