多普勒流量测量概述-信号解调方法等

　　1.2.2多普勒信号解调方法

　　CW Doppler流量测量中换能器接收到的信号可认为是多个多普勒频移成份的叠加，表述为：

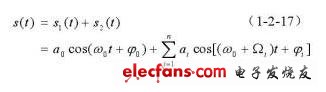
　　式中ai为频移分量幅值，Ωi为频移分量的频率，φi为频移分量的初始相位，s1（t）为经管壁、衬里等非运动介质耦合到接收探头的信号。

　　多普勒信号解调的目的在于提取频移信息，理想的解调应当取得正比于

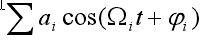
　　的输出。目前常用的解调方法有振幅检波、鉴频、鉴相及乘法器检波等四种，但由于s（t）受多普勒频移成分的非线性调制，振幅检波、鉴相检波两种解调方式将产生失真，鉴频检波输出的电压幅值中将包含与频移Ωi成正比的量，也不可取。乘法器检波用参考信号cosω0t与接收信号s（t）相乘，再用低通滤波器滤除高频分量，得到输出：

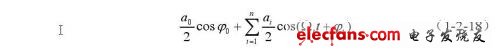
　　这种方法得到的输出没有引起失真，因此在传统的工业管道超声多普勒流量计中得到了广泛的使用。

　　1.2.3流速方向信息提取

　　现有工业管道超声多普勒流量计均不能判断流速的方向，在医学血流测量领域，流速方向信息的提取主要有时域法、频域法和相域法，分别介绍如下：

　　（1）时域法

　　基本原理是将接收到的超声多普勒信号s（t）同时送入两个乘法器，分别与有一定相位差β0的两个同频信号cosωot和cos（ω0t +β0）相乘，再低通滤波除去高频分量，于是得到第一路的输出为：

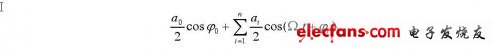
　　第二路的输出为：

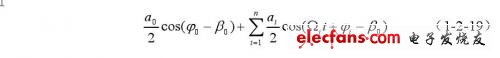
　　若血流方向为正，则Ωi》0 ，第一路输出的相位超前第二路输出的相位；若血流方向为负，则Ωi《0，第二路输出的相位超前第一路输出的相位。因此比较两路输出在时间上的先后就可以检测出血流的方向信息。

　　（2）频域法

　　超声波经血流散射后，其频谱位于发射频率ω0的两侧。血流方向为正时，回波信号频率高于ω0，成为上边带；血流方向为负时，回波信号频率低于ω0，成为下边带。频域法方向检测的关键是制作性能优良的高频上、下边带滤波器分离频谱的上下边带，使得正、反向血流信号分别在两个通道中输出

　　（3）相域法

　　假设超声多普勒回波信号表示为：

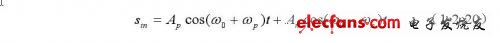
　　式中脚标p，n分别表示正向和反向血流。

　　相域法分离正、反向血流信号的框图如图1-4所示。

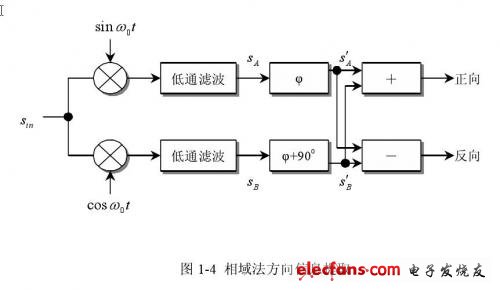
　　用两个同频正弦正交信号对输入信号进行解调，并低通滤波除去高频分量后得到：

　　经过两个全通移相网络，得到：

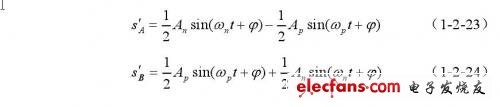
　　正向输出为：

　　反向输出：

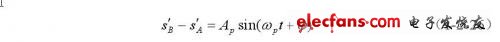
　　这样就完成了正、反向血流信号的检测和分离。相域法需要保证两路通道中低通滤波器和移相网络增益的严格对称，实现起来比较复杂。

　　1.2.4频谱估计方法

　　传统超声多普勒信号的频率估计常采用零交叉计数法和快速傅立叶变换法（FFT）等经典谱估计算法，这些方法存在频率分辨率低，旁瓣泄漏严重等缺点。为克服这些问题，以参数模型为基础的现代谱估计方法得到了很大的发展，并在超声多普勒血流测量中得到很好的应用。参数模型法的思路是假定需分析的多普勒信号 x（n）（n= 1，2，。..，N ）是一个输入序列u（n）激励一个线性系统H（z）的输出，由已知的x（n）估计H（z）的参数，再由H（z）的参数来估计x（n）的功率谱。x（n）和 u（n）之间有如下的输入输出关系：

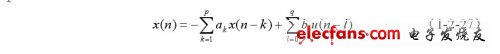
　　式中b0 =1，若b1，b2，。..， bq全为零，则为AR（Autoregressive）模型；若a1，a2，。..，ap 全为零，则为MA（Moving Average）模型；若a1，a2，。..，ap， b1，b2，。..，bq 不全为零，则ARMA（Autoregressive Moving Average）模型。当参数模型为AR模型时，H（z）和功率谱Px（ejω）分别表述如下

　　式中σ2为u （n）的方差。AR模型的系数求解算法有自相关法、Burg算法和改进的协方差（MCOV）算法等。采用MCOV算法时，AR模型的参数可以通过求解改进的协方差方程组进行估计：

　　式中fs是采样率。采用这种方法时，计算复杂性会随着阶次p的增加而增大。确定阶次p的常用方法有最终预测误差准则和信息论准则等。血流分析中，根据多普勒信号的特点，一般取阶次p=4。

　　1.2.5数字信号处理技术

　　DSP器件采用并行的总线结构，运算速度快、集成度高，于20世纪80年代初出现，到20世纪90年代中后期开始高速发展，近年来在超声多普勒血流测量领域受到高度重视，被广泛用来分析多普勒信号的频谱。另外，在数字信号处理中也有人用FPGA（Field Programmable Gate Array）来实现一些比较固定的算法，如FFT、FIR（Finite Impulse Response）滤波等。

采用高速DSP以及FPGA等器件的系统设计方法使得传统基于硬件的设计转移到基于