OPTIMUS应用于电动机控制系统优化技术
时间:05-26
来源:本站整理
点击:
1. 问题阐述
应用概述
电动机控制系统的设计是一个涉及多学科的问题,包括机械、电气和控制系统。OPTIMUS 能探索设计空间并通过其强大的优化算法在不需要用户干涉的情况下自动改进设计。本应用案例演示了OPTIMUS 如何与Simulink 集成在一起,通过修改(a)电动机的磁极宽度 (b)激励信号,来优化电动机的输出扭矩波纹和开关损耗。
设计问题
控制系统的模型在Simulink 中建立。电动机不同磁极宽度对应的电磁场已经在ANSYS 中计算完成,而线圈电感作为结果被导入到Simulink 的模型中。逆变电路在PSpice 中完成建模,然后通过SLPS 接口将电路模块转换为与Simulink 兼容的模块,由此完成了集成。
使用的软件工具
• OPTIMUS 及其Matlab/Simulink 接口
• Simulink
• PSpice (SLPS 接口)
• ANSYS
仿真过程与OPTIMUS工作流OPTIMUS 图形用户界面集成了仿真程序,它们的工作流程以及输入输出文件。通过OPTIMUS 与Matlab/Simulink 的接口,OPTIMUS很方便地参数化了仿真的输入文件,并从输出文件中解析出需要的输出参数(图 1)。
模型
案例中的电动机是3 相激励、6 极静子、4 极转子的开关磁阻电动机(SRM)。控制系统仿真在Simulink 中建立,电动机电磁场在ANSYS 中计算,逆变电路在PSpice 中建模。(图2)
3 个设计参数分别是电动机磁极宽度、激励信号的起始角度和激励信号的宽度。优化目标是最小化电动机输出扭矩的波纹。约束条件是电动机转速大于1000RPM。
方法应用
试验设计与响应面模型
试验设计(DOE)方法 与响应面模型(RSM)被用于探索设计空间。在本案例中,应用了100 个样本点的拉丁超立方 方法。在此基础上,建立了基于泰勒多项式的 最小二乘响应面,来拟合试验设计样本点。
设计优化
OPTIMUS 在本案例中应用了自适应进化(SAE)遗传算法,通过在响应面上求解来找到最小的电动机输出扭矩波纹,同时也满足电动机转速不低于1000 RPM。在响应面上求出的最优解,在接下来在仿真工作流求解的局部优化过程中,被用作起始点。这样,通过几个优化算法、不同求解方式的策略化结合,使得最后能够找到全局最优设计,同时缩短了优化过程的时间。
结果阐述
试验设计和响应面模型
拉丁超立方试验设计方法被运行来最为建立相应面的样本。图4 显示了电动机磁极宽度和激励信号宽度是对输出扭矩波纹有较大影响的重要设计参数。这个响应面模型是对仿真模型的近似。在优化过程中,如果需要连续大量求解仿真模型,会需要相当大的计算量。适当地使用响应面模型能有效降低计算量,提高优化过程的效率。响应面模型的质量(及其对于优化过程可靠性)可以通过在建立过程中得到的回归系数进行确认。
结论
OPTIMUS 成功地自动化了Simulink仿真,并找到了最优的磁极宽度、激励信号的起始角度和宽度,使得电动机的输出扭矩波纹得到了有效降低,并且保证了电动机转速始终高于规定转速。
收益
• 自动化现有的仿真流程
• 将工程师从重复性的劳动中解放出来
• 设计空间探索和强大的优化方法帮助找到最优设计并且满足约束条件。
应用概述
电动机控制系统的设计是一个涉及多学科的问题,包括机械、电气和控制系统。OPTIMUS 能探索设计空间并通过其强大的优化算法在不需要用户干涉的情况下自动改进设计。本应用案例演示了OPTIMUS 如何与Simulink 集成在一起,通过修改(a)电动机的磁极宽度 (b)激励信号,来优化电动机的输出扭矩波纹和开关损耗。
设计问题
控制系统的模型在Simulink 中建立。电动机不同磁极宽度对应的电磁场已经在ANSYS 中计算完成,而线圈电感作为结果被导入到Simulink 的模型中。逆变电路在PSpice 中完成建模,然后通过SLPS 接口将电路模块转换为与Simulink 兼容的模块,由此完成了集成。
使用的软件工具
• OPTIMUS 及其Matlab/Simulink 接口
• Simulink
• PSpice (SLPS 接口)
• ANSYS
仿真过程与OPTIMUS工作流OPTIMUS 图形用户界面集成了仿真程序,它们的工作流程以及输入输出文件。通过OPTIMUS 与Matlab/Simulink 的接口,OPTIMUS很方便地参数化了仿真的输入文件,并从输出文件中解析出需要的输出参数(图 1)。
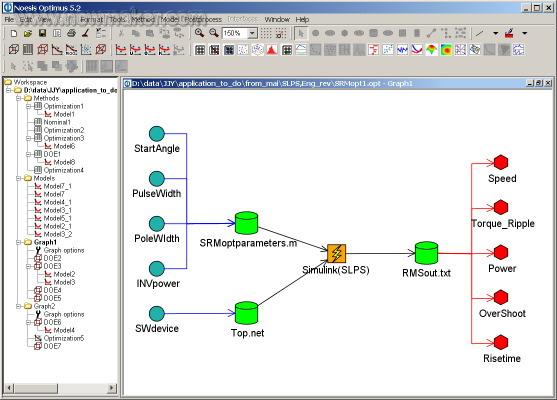
图 1 – 电动机控制系统仿真的OPTIMUS 工作流
模型
案例中的电动机是3 相激励、6 极静子、4 极转子的开关磁阻电动机(SRM)。控制系统仿真在Simulink 中建立,电动机电磁场在ANSYS 中计算,逆变电路在PSpice 中建模。(图2)
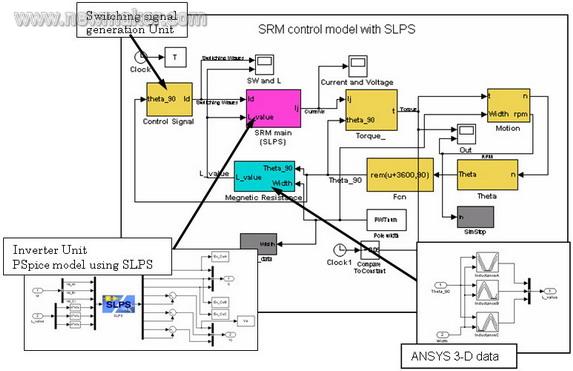
图 2 – 电动机控制系统的Simulink 模型
3 个设计参数分别是电动机磁极宽度、激励信号的起始角度和激励信号的宽度。优化目标是最小化电动机输出扭矩的波纹。约束条件是电动机转速大于1000RPM。
方法应用
试验设计与响应面模型
试验设计(DOE)方法 与响应面模型(RSM)被用于探索设计空间。在本案例中,应用了100 个样本点的拉丁超立方 方法。在此基础上,建立了基于泰勒多项式的 最小二乘响应面,来拟合试验设计样本点。
设计优化
OPTIMUS 在本案例中应用了自适应进化(SAE)遗传算法,通过在响应面上求解来找到最小的电动机输出扭矩波纹,同时也满足电动机转速不低于1000 RPM。在响应面上求出的最优解,在接下来在仿真工作流求解的局部优化过程中,被用作起始点。这样,通过几个优化算法、不同求解方式的策略化结合,使得最后能够找到全局最优设计,同时缩短了优化过程的时间。
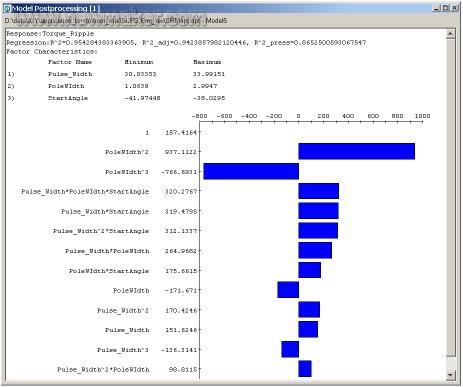
图3 – 贡献度图显示了电动机磁极宽度与激励信号起始角度是对输出扭矩波纹影响最大的设计参数
结果阐述
试验设计和响应面模型
拉丁超立方试验设计方法被运行来最为建立相应面的样本。图4 显示了电动机磁极宽度和激励信号宽度是对输出扭矩波纹有较大影响的重要设计参数。这个响应面模型是对仿真模型的近似。在优化过程中,如果需要连续大量求解仿真模型,会需要相当大的计算量。适当地使用响应面模型能有效降低计算量,提高优化过程的效率。响应面模型的质量(及其对于优化过程可靠性)可以通过在建立过程中得到的回归系数进行确认。
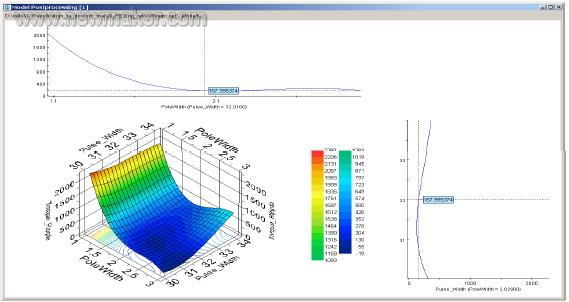
图4 – OPTIMUS 建立响应面显示了输出扭矩波纹与选择的输入参数之间的变化关系
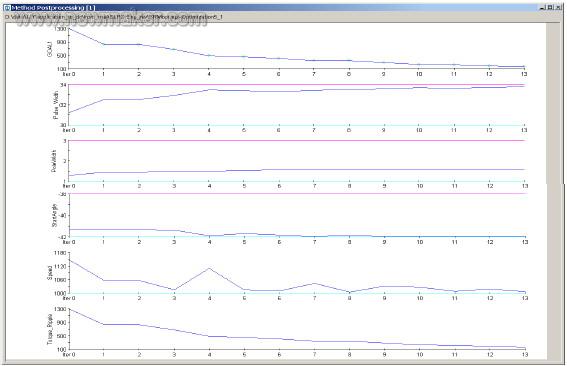
图5 – 优化目标函数的收敛: 最小化输出扭矩波纹
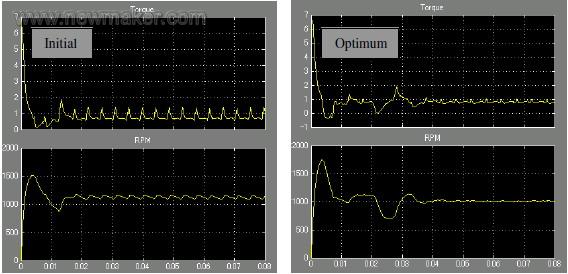
图6 – 优化前后的电动机的输出扭矩和转速
结论
OPTIMUS 成功地自动化了Simulink仿真,并找到了最优的磁极宽度、激励信号的起始角度和宽度,使得电动机的输出扭矩波纹得到了有效降低,并且保证了电动机转速始终高于规定转速。
收益
• 自动化现有的仿真流程
• 将工程师从重复性的劳动中解放出来
• 设计空间探索和强大的优化方法帮助找到最优设计并且满足约束条件。
- 电动 / 混合电动汽车电池管理系统的可靠性(11-09)
- 简易智能电动车及电源电路设计(12-09)
- 基于LabVIEW的电池管理系统监控平台开发(01-26)
- 电动汽车燃料电池增程器的系统集成设计(10-08)
- CAN和光纤实现电动汽车动力电池组采集系统(10-20)
- 动力电池参与电网调峰的研究(10-26)
