弓箭手打靶为什么不总是打到红心？

赛场上我们时常见到弓箭手或者枪手打靶，每个弓箭手在打靶之前都进行了许多准备，瞄准、调整心态，但是命中的靶总是离靶心有一定距离，这是怎么回事呢？有的人会说这个是因为误差问题，那大家想过没有，这个所谓的误差是如何导致的呢？

一、误差的基本概念及分析
在系统测量中我们知道被测量的真实值称为真值。在一定的时间和空间内，真值是一个客观存在的数值。在测量过程中，即使选用精度最高的测量器具、测量仪器和仪表，并且没有人为的失误，要想测得真值也是不可能的。况且由于人类对客观事物的认识的局限性、测量方法的不完善性以及测量工作中常有的各种失误等，更会使测量结果与真实值之间存在差别，这种差别就叫做测量误差。

图 1 射击误差

二、测量误差分类
测量误差按照其性质和特点，可分为系统误差、偶然误差（随机误差）和疏失误差三类。

系统误差

在相同的测量条件下，多次测量同一个量时，误差的数值（大小和符号）均保持不变或按某种确定性的规律变化的误差称为系统误差。系统误差通常是由于测量器具、测量仪器和仪表本身的误差产生的。此外，由于测量方法的不完善性和测试者测试习惯产生的误差也称为系统误差。

系统误差的大小可以衡量测试数据与真值的偏离程度，即测量的准确度。系统误差越小，测量的结果就越准确。

偶然误差

在测试过程中，由于某些偶然因素而引起的误差称为偶然误差，也叫做随机误差。比如：电磁场的微变、温度的起伏、空气扰动、大地的微震、测量人员的感官无规律的微小变化等。这些变化是人们无法掌控的，是无规律的，这导致测量结果不可能完全相同，如果相同也只能说明仪器灵敏度不够。

虽然偶然误差是不能够被人们消除的，但是偶然误差是符合正态分布的。即测量误差小的出现概率大，而误差相对大的出现概率小，并且大小相等的正负误差出现的概率也是相等的。

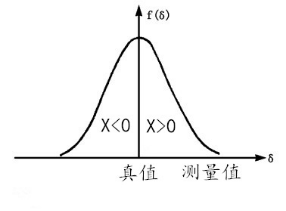
图 2 偶然误差的概率曲线

疏失误差

由于测量者的疏忽过失而造成的误差称为疏失误差。它产生的原因主要有两点：其一是实验者本身造成的；其二是由于测量条件造成的。

在测试过程中，由于操作者的粗心或不正确操作，例如：读数或记录错误、操作方法不对、测量方法不合理等，这些测量值误差太大，一半被称为"坏值"，应该舍去。

三中误差比较

这三种误差的不同可以以打靶为例，图3-a中的弹着点均匀在靶心，这说明没有系统误差，但分布分散说明偶然误差较大。图3-b中的弹着点偏于靶心，说明系统误差较大。图3-c中的弹着点密集于靶心，说明只有偶然误差，没有系统误差。

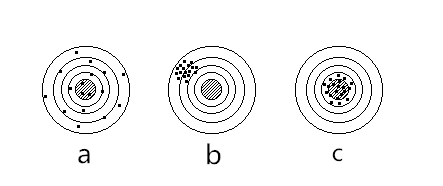
图 3 用打靶说明三种误差

三、测量误差的表示方法和仪器精度的标定
1）绝对误差
打靶的靶心我们称之为真值，而我们打到的靶称之为测量值，而两者之差就是绝对误差。
2）相对误差
绝对误差只能表示某个测量值的近似程度。但是，两个不同大小的测量值，当他们的绝对误差相同时，准确程度并不同。例如：测量从北京到广州的距离，误差为1米，这是误差就不大，可是如果测量从天安门广场到人民大会堂的距离，误差为1米，这时误差就比较大了。为了更加符合习惯地衡量测量值的准确程度，便引入了相对误差的概念。
绝对误差与被测量真值之比，称为测量值的相对误差。
3）仪器误差及准确度
仪器精度在标定时也类似于打靶，绝对误差和相对误差是从误差的表示和测量的结果来反映某一测量值的误差情况，但并不能用来评价测量仪表仪器的准确度。
当仪表在规定的正常条件下工作时，其示值的绝对误差与其量程之比称为仪表的引入误差，因为引用误差以量程为比较对象，因此也称为基准误差。测量仪表在整个量程范围内所出现的最大引用误差，称为仪表的容许误差，。仪器仪表的技术说明书中标明的误差都是指的容许误差。
对于指针式仪表，设容许误差的绝对值为

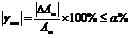
式中---仪表的准确度等级，它表明了仪表容许误差绝对值的大小，也就是我们平时所说的精度，也可以理解为打靶人的技术能力。

系统误差的消除方式

消除由测量仪器和仪表引入的误差

在测量过程中，要根据测量的准确度的要求选择不同准确度等级的仪器、仪表；

消除由于测量方法或理论分析所引起的误差

在测量前没有充分考虑，但在测量中参与作用的一些因素所导致的误差，经常是由于理论分析不充分或者时由于采用了近似公式所引起的。这些情况应设法避免。

消除由测量人员所引起的误差

由实验者的反应速度和固有习惯等生理特点所引起的误差属于人为误差。如记录一个信号时，观测者有超前或滞后的倾向，而且倾向因人而异，这必然导致误差