是德科技：浅谈混频器的相位特性测试

振的相位对混频器相位传输特性的影响为扫频范围内一个固定的相移，相当于混频器的相位特性曲线向上或者向下平移了一定的位置，对于曲线的斜率以及不同频点上的相位差是不影响的，那么它对于混频器的时延特性和相位非线性也没有影响，可以忽略不计。

如果混频器的本振是扫描的，那么本振在不同频点处的相位变化将会影响到混频器相位特性曲线的斜率，进而影响到混频器的时延。然而当混频器本振处于扫描状态时，其输入或者输出必定有一个是固定的。假设输入信号和本振同步扫描，输出固定，那么在输出端增加的延迟（比如增加一段传输线）只能表现为一定的相移而无法呈现出相位相对频率的函数，因此在测试时体现在混频器相位特性曲线上的也仅仅是一个相移而不是斜率的变化，这对于我们关注的混频器从输入到输出的时延特性是相悖的。因此，当混频器的本振处于扫描状态时，通常会改变测试的思路，由于器件在输出频率处都会有一定的带宽，可以将输入信号扫频的范围分成若干个小段，而本振变成步进的状态，在每个分段中采用固定本振的测试方法得到每个带宽范围内器件的时延，将所有分段中心频点处的时延连起来，就能够拼接成本振扫描状态下的器件时延。

现有的混频器时延或相位非线性测试方法主要有向下/向上变换（三混频器）法，调制信号法（包括双音法），矢量混频器测试法（VMC）和相位相参接收机测试法（SMC+ Phase）等。

3.1.向下/向上变换法

该方法是采用一个额外的与被测混频器（MUT）频率范围相同，变频方向相反的逆变换混频器，比如MUT是下变频器（从RF变到IF），那么逆变换混频器就是上变频器（从IF变到RF），两者本振共享。将两个变频器串联后形成的链路，输入和输出信号则是同频的，可以直接用网络分析仪进行幅度和相位测试，得到串联后链路的传输特性，即为MUT和逆变换混频器传输特性的乘积。

如果再找到一个与MUT频率范围相同的互易混频器（可以上变频也可以下变频，两个变频方向的传输特性一致，即SC21=SC12），将该混频器作为上变频器与MUT串联，同样可以得到串联后的传输特性，即为MUT和互易混频器传输特性的乘积。

然后将该互易混频器作为下变频器与第一步中的逆变换混频器串联，则能够得到互易混频器和逆变换混频器传输特性的乘积。

考虑到混频器的工作特点，为了防止镜像信号也被逆变换混频器或者互易混频器转换到输出频段，在下变频器的输出端需要采用一个带通滤波器。

假定互易混频器为A，逆变换混频器为B，MUT为C，测试原理图如下：

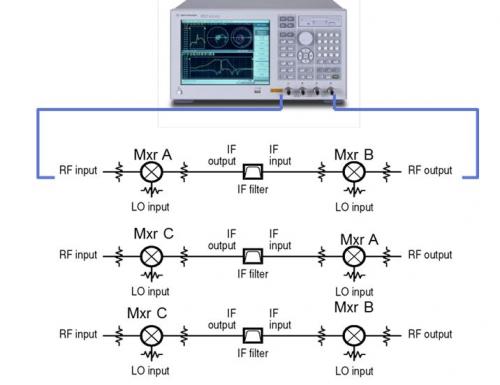
图3.三混频器法原理图

在不考虑失配影响的情况下，三次测试的传输特性G1、G2、G3与混频器的传输参数有如下关系（此处的所有参数均为复数，包含幅度和相位特性）：

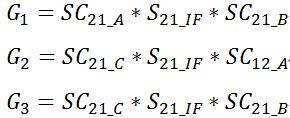
由此可得每个混频器的传输参数：

被测混频器C的相位特性可以由下式计算得到：

进行开方运算时，需要根据实际情况选取正确的平方根。

该方法原理上很简单，普通的矢量网络分析仪即可完成测试。不过它也有一些不足之处：

步骤较多，而且需要两个额外的混频器，其中一个还要是互易的。当测试频率提高到微波或毫米波频段时，很难找到合适的互易混频器。 所有的混频器必须共用同一个本振源，因此当被测混频器的本振无法由外部提供时，该方法将无法完成测试。 忽略了混频器和IF滤波器之间端口失配的影响，测试结果误差较大。

在此方法的基础上，如果能够提取出互易混频器的散射参数，那么只需要测试被测混频器和IF滤波器以及互易混频器串联链路的S参数，然后采用去嵌入的算法消除互易混频器和IF滤波器的影响就能得到被测混频器的散射参数。Keysight公司的ENA系列矢量网络分析仪即采用了这种方法，测试过程中只需要增加一个额外的互易混频器和镜像抑制滤波器。测试框图如下，互易混频器的参数提取方式将在3.3节中介绍。

图4.ENA矢量混频器测试框图

3.2.调制信号法

前文中提到，如果不考虑输入输出频率的变化，混频器也可以近似看作为线性器件，在它的输入端加一个调制信号，比如AM调制，输出端的信号也将呈现相似的包络起伏，输入信号的数学表达式如下：

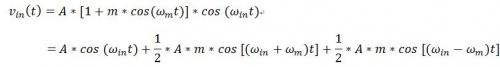
假设通过混频器后三个频率分量的相位分别变化了?0，?1，?2，如果在ω_in-ω_m到ω_in+ω_m范围内混频器的相位特性是线性的（有相同的时延），那么三个频点的相位变化量满足如下关系：

则输出信号为：

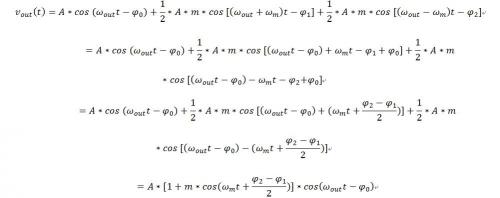
输入端与输出端的包络之间的相位差为(φ_2-φ_1)/2，由此可得混频器在当前载波频点处的传输时延：

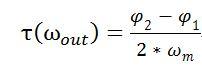
因此，如果给混频器的输