利用Teledyne LeCroy示波器测量噪声

声时限制了带宽。参数P7中测量出波形F3的面积的平均值是23.26mV2。 这和参数P8中显示的波形C1的平方值的平均值23.23mV2 是一致的。

如图5所示，将光标放在F2上可以直接读出该点的功率谱密度。图中光标在10MHz，此刻功率谱密度是689.49 pV2 /Hz。

参数统计结果包括了最小值和最大值。如果您想查看多次连续捕获的参数值的变化过程，可以使用Trend函数。Trend按测量的次序从左到右依次画出每次测量的参数值。图8显示的例子中F4是参数P1的趋势图，反应了通道1波形的标准偏差的变化趋势。每捕获一次会得到一个标准偏差值，F4显示出按次序测量的逐次结果。Trend波形可以当作是任何其它波形一样再进行测量和分析。

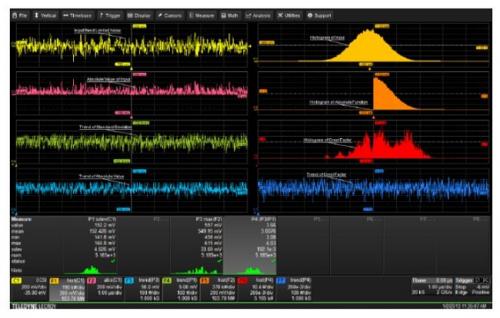
图8 利用参数运算测量出振幅因数,以及直方图和趋势图的每个步骤

推导出来的测量参数
另外一个感兴趣的噪声参数是振幅因数，即波形的峰值和有效值的比值。振幅因数决定了信号中峰值变化的动态范围。虽然示波器中没有双极性的"峰值"参数，我们可以通过通道1中的信号的绝对值"创造"一个这样的参数值。将负值翻转到波形的正区域，然后使用最大值参数得到每次捕获的正向正大值和负向最大值中的极大值。请注意这种方法可以行得通是因为信号平均值为零。 我们可以利用参数数学运算来计算出振幅因数。参数数学运算的设置如图9所示，我们计算出振幅因数结果为参数P4，是P3和P1的比值。测量结果如图8所示，得到的结果平均值是3.6。图8中F6显示出参数P4的直方图，其分布并不是高斯的，这是由绝对值和最大值的数学运算有关的非线性过程引起。

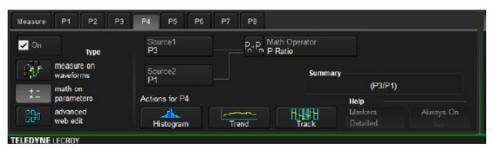
图9 利用参数运算功能测量振幅因数

利用nbpw测量单点噪声
另外一种对噪声进行单点测量的方法是采用光领域的窄带功率测量(Narrow-band power,nbpw)方法。nbpw通过计算某个频率点的离散傅立叶变换来测量该频点的功率。输出单位是dBm。该方法对于测量噪声并不是很非常方便，我们更喜欢使用线性单位V2 /Hz的噪声功率谱密度来测量。幸运地是，Teledyne LeCroy示波器能够嵌入算法来对参数进行更复杂的运算以得到需要的测量结果。这比图9中振幅因数的简单比例参数要复杂得多。这个测量结果如图10所示。

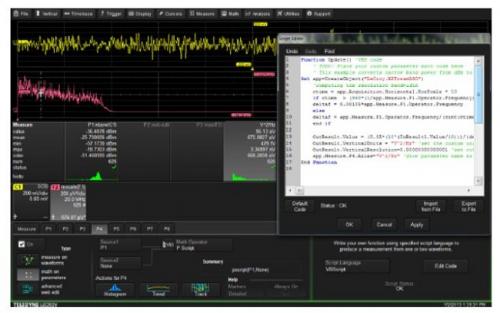
图10 改变nbpw测量的刻度以得到单位是V2/Hz的功率谱密度

参数P4用V2/Hz进行重新定标，是100KHz时的功率谱密度，它是基于参数P1的nbpw测量进行重新调整刻度的结果。基于1000次测量的P4的平均值可以和基于平均后的FFT的测量结果做比较，FFT的结果可以用绝对光标卡在函数波形F3上读出。 这两个数值在仪器精确度限制范围内是具有可比性的。

图11显示了用于编辑测量参数计算代码的对话框。代码可以用VB或Java语言来编写。

图11 设置参数计算代码的测量对话框，将参数P1归一化到V2/Hz

图12 给出了本例中用于重新定标nbpw 参数的VB 代码。

图12 参数运算的VB代码，将nbpw结果由dBm转换为V2/Hz

代码算法分别将每个nbpw测量结果由对数转换为线性的刻度(V2)，读出捕获的数据长度，然后计算出FFT的有效分辨带宽。接下来，算法中利用这个值得到单位是V2/Hz的功率谱密度。

伪随机序列长度
如果您在研究的是伪随机序列噪声源，您可以轻松地使用Teledyne LeCroy示波器的光相关函数测量序列间隔。

图13中利用了波形C1的自动相关函数表示这种测量的结果。自动相关函数产生的峰值点和伪随机码型的重复周期相对应。本例中，参数P7测量出码型周期是131us。这和125MHz的时钟频率的16384个时钟周期序列长度是一致的。

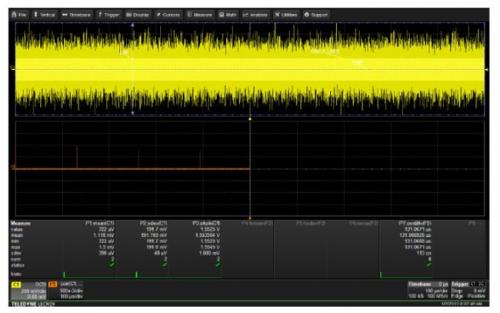
图13 利用自动相关函数来确定伪随机序列的长度

Teledyne LeCroy示波器拥有噪声测量的时域，频域，统计域的一切必要的工具，对于熟悉这种类型测量的工程师来说提供了很大的灵活强大的分析能力。