一种应用于足浴器的温控器的研制

介绍了一种基于单片机应用于足浴器的自动控温系统的实现原理及方法。该控温系统利用51系列单片机，由开关电源高效稳定供电，通过外围引脚中断、定时器、PID算法、DS18B20温度传感器，实现了温度实时显示，按键调节设定温度功能，解决了加热及冷却过程中热过冲与过冷问题。其成本低、控温精度高、温度可调、运行稳定可靠。

足浴器的设计难点在于成本控制和温度控制系统的设计。近年来，开关电源技术的逐渐成熟，为小功率电源供电提供了一个高效率且低成本的方案，摒弃了传统的变压器降压、整流、三端稳压的低效率供电方式。而通过软件算法完善，例如PID算法的运用，可减少部分硬件开销，降低成本及系统复杂度，提高系统的稳定性。设计结合以上技术，着眼于成本最小化，性能最大化，实现了LED温度显示，双按键目标温度调节，高精度温控功能。由于主控芯片AT89C2051只有两组共16个IO引脚，2 kB的内存，因此需合理运用IO资源，程序设计简洁，合理分配内存空间。

1 系统结构设计
系统由供电、采样、按键、显示及单片机部分组成。

传感器负责采集温度值，传递给MCU，目标值由按键设定，MCU将采样值与目标值进行比较，经过时间PID算法处理，根据每段时间不同的温差值，计算出需要加热的时间，接着通过IO口控制继电器闭合与断开，使加热板工作，同时LED显示实时温度。

2 子模块的设计
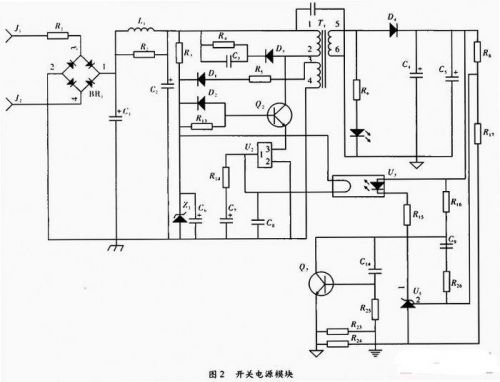
(1)供电模块。供电部分采用开关电源技术，采用开关电源可以解决传统变压器所带来的问题，整个设计可变得简洁；供电效率高，且稳定；并可减少系统结构体积。由于传统的基极驱动方式会将普通NPN型开关晶体管的安全工作电压限定在BVceo，而采用射极驱动的方式，可将安全工作电压从Vceo扩大到Vcbo，由于BVcbo>BVceo，即可改善NPN型晶体管的安全工作范围，对市电为220 V的电网电压可用普通的NPN型功率开关管。该电路接通交流220 V经整流桥后，形成直流电压，R2为启动电阻，开关管用NPN管，输出电流及输出电压信号通过光隔U3反馈至射极驱动芯片U2，U2根据信号调节控制开关管的占空比，使得输出保持稳定。

(2)采样模块。采样部分采用DS18B20，其为美国Dallas生产的一线可编程数字温度传感器。它不同于传统的模拟温度传感器，其可产生对应温度的数字信号，与主控芯片只需单线通信，使得系统结构简单可靠。由于通信线为双向输入输出的OC门，因此需外加一个上拉电阻到VCC。DS18B20与MCU通信的时序要求严格，所以在采样过程中有必要关闭MCU的中断功能，防止外部干扰导致采集到错误数据。
(3)控制模块。控制部分南同态继电器(SSR)实现弱信号对强电的控制。由于固态继电器内部光耦合器的应用，使其控制信号所需的功率较低，且所需工作电压与TTL，CMOS等常用电平标准兼容，可实现直接连接。SSR工作时无机械动作，其具备了传统的"线圈-簧片触点式"继电器(MER)所没有的优点，即工作可靠性高，寿命长，此外，SSR还具有可承受比额定电流高约10倍的浪涌电压的特点。考虑到51系列单片机IO口驱动能力较弱，在原理图设计上需要外加PNP开关管，如图3所示。

(4)算法模块。热电阻丝具有过冲过冷现象，采用软件的PID算法可以弥补硬件部分的不足。PID算法是一种比例、积分、微分并联应用广泛的一种模糊控制算法。PID算法的数学模型可用下式表示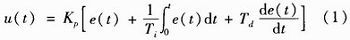


其中，Kp为比例系数；Ti为积分系数；Td为微分系数；e(t)为采样值与目标值的偏差。比例部分由式Kp*e(t)表示。若Kp越大，则过渡过程越快，也易产生振荡。因此Kp选择恰当，才能起到快速过渡且又稳定的效果。积分部分为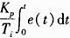。从表达式可知，只要存在偏差，则积分部分的控制作用就会不断增加，只有在偏差部分e(t)=0时，积分表达式才会为一个常数。其中积分时间Ti对积分控制的影响较大。Ti越大时，积分效果越弱，消除偏差需要的时间也越长。Ti越小，则积分效果较强，消除偏差需要时间也越短，但是容易在消除过程中产生振荡。
微分部分表达式为
微分部分的作用为抑制偏差变化。Td越大，则抑制能力较强；Td越小，则抑制能力较弱。显然微分部分对系统的稳定性有较大的作用。

由于计算机无法像模拟控制那样连续输出控制量，进行连续控制。所以上式需进行离散化处理。离散化的思路为：以T作为采样周期，将连续时间t分为k个采样周期，即t=kT，将t代入式(1)可得到离散PID表达式


采用增量式PID算法的优势在于可减少计算机的计算任务，并且增量式算法只取决于目前时刻，上一时刻，上上时刻的值，对起始参数不敏感。
3个系数的取值取决于实际经验，为达到较好的控制效果，因此在各温度区域由实验测取了最佳PID控制参数值。系统PID算法流程如图4所示。
由图4可知，若输出值为x，则2 s内的需加热时长为x×20 ms，不加热时长为(2 000-x·20)ms。