电弧炉谐波检测仪的设计研究

O 引 言

　　电弧炉等各种非线性设备会产生谐波。在电力系统中，高次谐波产生了多余的谐波损耗，使各种电力设备的效率降低，其带来的波形畸变严重影响了电能质量，并且在某些信号传输的过程中产生了干扰。对谐波信号进行实时在线的有效检测，有助于谐波消除的实现，其为进行电弧炉的各种控制以及有源滤波器的设计提供有效的支持。

　　现有的频谱分析装置对于电力系统的谐波频谱虽然可以达到所需的要求，但是成本过高且不宜携带，尤其是具体的电弧炉系统会产生的大多为几十次的谐波．更大次数的谐波由于幅度极小，可以被看成是系统中的噪声，没有必要在全频段进行谐波检测。此外，现有的电力系统谐波检测装置由于使用场合的不同，多以DSF芯片作为核心，而使用编程简单、成本更低的单片机芯片作为核心的很少。由于以上这两点，基于单片机芯片并且针对电弧炉系统的谐波检测装置的研究非常有必要。
　　电弧炉系统产生的谐波，不仅包括整数次谐波，还包括分数谐波和间谐波。一般来说，分数谐波(Frac-tion Harmonics)被定义为频率不等于基波频率整数倍的谐波分量，分为间谐波(Interharmonics)和次谐波(Subharmonics)。间谐波是指频率介于工频谐波之间的谐波分量；次谐波是指频率低于基波频率的谐波分量。电弧炉是电力系统中产生分数谐波的主要来源之一。在电网质量上，国际标准对分数谐波并没有明确的规定，但在电磁兼容标准IEC61000-3．6中，建议分数次谐波的电压应该限制在O．2％以下。另外，由于电弧的不规则游动以及电弧电阻的随机性，使得电弧炉系统的谐波分量也随时间随机变化。

　　在谐波检测的过程中，一般以谐波电流为目标进行检测。目前谐波电流检测的方法主要来源于基于模拟滤波器理论、瞬时无功功率理论、傅里叶变换、自适应控制理论、神经网络理论以及小波变换理论6种。其中，基于傅里叶变换的谐波检测方法，基于无功功率理论的谐波检测方法和基于神经网络的谐波检测方法都可以满足电弧炉对谐波检测的相关要求，例如实时性好，能满足精度等。

　　由于使用无功功率理论的谐波检测理论能够直接得到谐波信号的瞬时分量，更适合于直接补偿谐波分量以改善电网电力质量。相比之下，构造检测并显示谐波参数的环节更多采用基于快速傅里叶变换理论的方法，这里提出一种采用基于傅里叶变换的谐波检测方法进行检测仪的设计。该仪器以MSP430系列单片机为主要核心进行相关软硬件部分的设计，主要功能包括计算并显示电弧炉三相谐波电流的基波与各次谐波、功率因数、有效值以及有功无功功率等各项参数。

1 主要原理

　　要在电路中获得可以通过单片机计算的电流信号，必然先经过采样，变换为离散的数字信号。设有周期函数：

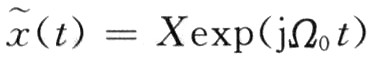
　　其中：Ω为频率；X为幅度；周期为T。以x(nT，)作为周期信号x(t)的抽样，每个周期内抽样N点，即T=NT，经傅里叶变换后形成变换对，简化后可表示为：

　　其中：，n∈(-∞,+∞)，k∈(∷∞，+∞)；X(k)的物理意义是序列x(n)第k次谐波分量的幅度。
在使用计算机或者单片机做信号处理方面的工作时，要求信号在频域和时域都是离散的，且都是有限长。离散傅里叶级数满足离散要求，但是在时域、频域虽然都是周期函数其也都是无限长的，所以在时域、频域中各取1个周期，可以得到傅里叶变换对：

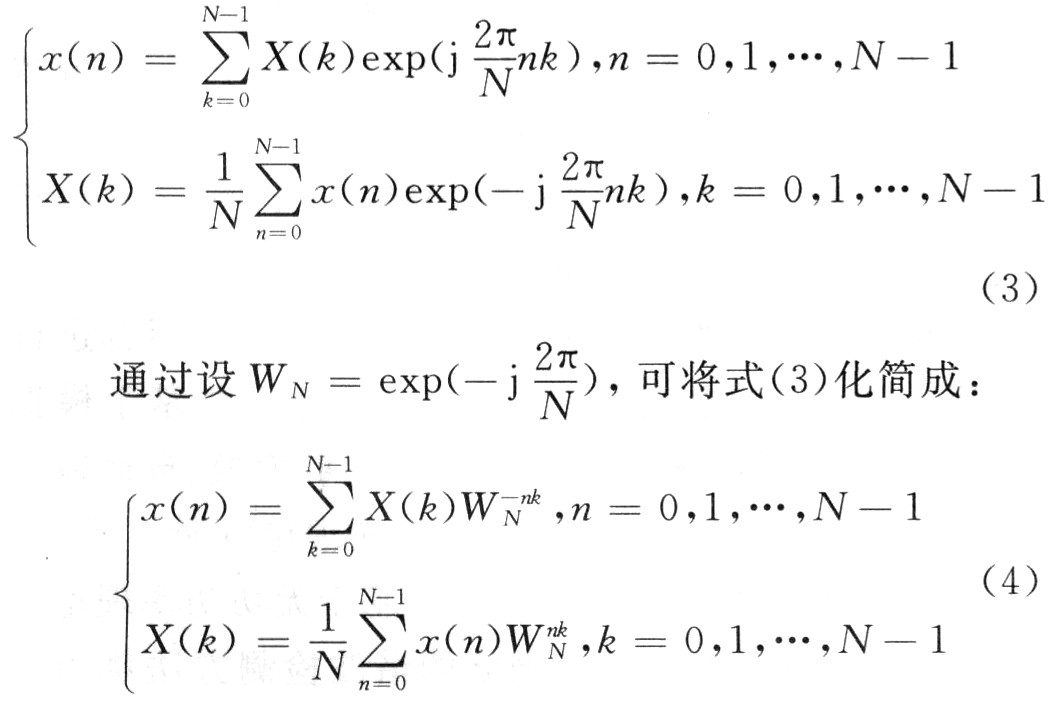
　　再根据快速傅里叶变换(FFT)理论，利用WN形成"蝶形单元"，经过分组、码位倒序等步骤计算，这样即可方便地通过计算机或单片机进行变换求其频谱。在此指出的检测谐波电流的仪器主要系统就是通过FFT方法计算出相应的谐波分量及其参数。

1．1 分数谐波的测量

　　可以看出，利用式(4)进行FFT可以准确地分离出被测电流中整数次谐波信号。正如在前文中所指出的，电弧炉系统中不仅包括整数次谐波，还包括大量分数谐波和间谐波。例如，对于频率为50 Hz的电网电流信号，其周期为20 ms，电弧炉作为负载可能还会产生出频率在50 Hz以下或者不为50 Hz整数倍的谐波。如果在检测时采样的时间正好为一个周期20 ms，则频率低于50 Hz的谐波信号就无法检测出来，在这里，可以通过延长采样时间的方法分理出分数次谐波。具体方法：对于基波频率为Ω，周期为T的电网电流信号来说，如果现在需要检测的是频率为Ω0／l的谐波分量(l为不为零的整数)，则采样时间必须为T1=lT。这样采样出来的序列可以看成是频率为Ω1=Ω/l的电流信号的1个周期；如果系统抽样频率不变，仍然是每T时间内抽样N个点，即T=NTs，则T1=lT=lNTS，可得：

这样，在进行相关的FFT变换过程，通过