基于 DSP 的电子负载：模糊自适应整定 PID 控制策略

4.3模糊自适应整定PID控制策略

在实际调试过程中，现场被控测试对象参数未知，电子负载电源板和信号板上打规模的模拟器件的引进，存在控制信号惯性滞后性，使得常规PID控制器往往不能达到理想的控制效果，为了进一步提高PID控制的性能，以适应复杂的工况和高性能指标的控制要求，模糊PID控制就是针对控制信号时延而提出的，将传统的PID调节技术和模糊控制技术相结合，利用模糊逻辑对PID调节器的参数进行调节以补偿模拟器件延时对系统的影响。因此，本系统引入模糊控制理论设计一个模糊PID控制器，根据实时监测的电压或电流值的变化，利用模糊控制规则自动调整PID控制器的参数。电子负载系统信号板控制的核心部件是MOSFET，在恒定的漏源电压下，它的漏极电流和栅源电压成非线性变化，而且随着漏源电流的变化导致MOSFET的温升，其转移特性曲线处于变化的过程中。在PID控制器中引入智能控制算法，使电子负载控制精度进一步提高，将对电子负载调试的经验作为知识DSP中，使DSP根据现场实际的情况，自动调整PID参数，成为具有PID参数自整定功能的智能调节器。

由于经验不易精确的描述，控制过程中各种信号及评价指标不易定量的表示，模糊理论是解决这一难题的最好方法，运用模糊控制规则，DSP根据电子负载系统的实际响应情况，运用模糊推理，实现对PID参数的自动调整，这就模糊自适应PID控制。以误差e和ec作为输入，根据偏差e和偏差变化率ec的变化，利用模糊控制规则在线对PID参数进行在线的修改，通过公式

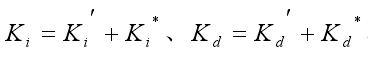
不断地调整PID控制器中三个参数，以满足不同时刻PID参数自整定的要求，其机构如图4.7所示。

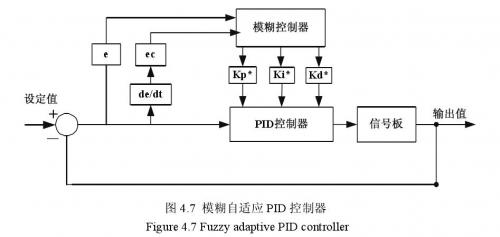
由于设计的电子负载只用到P和I两个参数，所以研究中，是在运行中通过不断的检测e和ec，运用模糊规则进行模糊推理，对P和I两个参数进行在线修改，从而使被控对象具有良好的动、静态性能。

模糊控制设计的核心是总结调试人员的技术知识和实际经验，根据现场的要求及被控对象的实际情况来选定模糊控制器的输入、输出变量，选取变量的论域和隶属度函数，建立合适的模糊规则表，通过查询模糊矩阵表解模糊后进行参数调整。Kp和K_I的模糊规则表见表4.3和表4.4.

（1）.输入/输出变量的论域在电子负载控制系统中，负载电流值偏差e和偏差变化率ec（以恒流高档位为例），其实际论域（基本论域）分别为

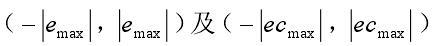
设定值为6A，取偏差值e的基本论域为（-0.04，0.04），偏差变化率ec的基本论域为（-1，1）。控制量的基本论域为（-1，1）。控制量的基本论域为

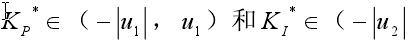
其基本论域的选择（根据经验值获得）分别为:K^*_P∈（-0.035，0.035）和K^*_I∈（-1.35，1.35）。

在具体选择模糊变量论域时，既要考虑到各模糊子集能够很好地覆盖论域，又要防止出现失控现象，同时又不能够随意地增加论域中元素的个数。如果论域中元素过多，虽然系统的控制精度得到提升但是却大大地增加了DSP工作量可能会导致系统的运行速度过慢。因此，选择具体的模糊变量论域时，必须兼顾论域的覆盖率及DSP的运算能力，其实际值在本系统中为（-6，-5…0，1，…6）十三个等级。

（2）。量化因子和比例因子

控制系统每次采样获得的采样值都需要乘上一个相应的因子，使得输入变量能够从其实际论域转换到模糊论域中，这就是量化因子K的概念。一般地，用Ke，Kec分别表示系统的偏差e和偏差的变化率ec的量化因子。根据前述可知，电流偏差e和偏差变化率ec的实际论域分别为（-|e_max|，|e_max|）及（-|e_cmax|，|ec_max|），所有变量的模糊论域同为（-n，-n+1，…0，1，…n）那么，Ke、Kec可由下式确定，即：

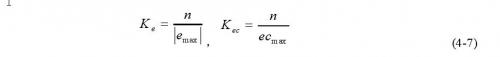
通过模糊推理获得的输出不能直接作用于被控对象必须通过解模糊接口将其转换为被控对象所识别的基本论域中。由前述可知系统控制量的基本论域为，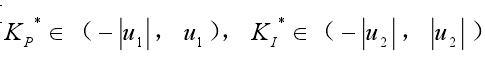

则其比例因子Kup、Kui分别为：

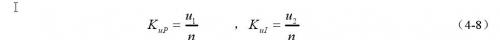
获得了比例因子之后，最终输出给被控对象的任一实际控制值可以由下式求得：

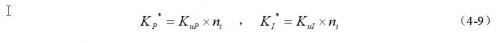
其中K^*_P、K^*_I分别表示模糊控制器最终输出给PID控制器参数的调整因子。

根据以上给出的公式及数据，可以分别求出本系统的量化因子和比例因子，Ke =150，Kec = 6，Kcp = 0.006，Kui = 0.225.输入e和ec量化表如下表4.1所示。

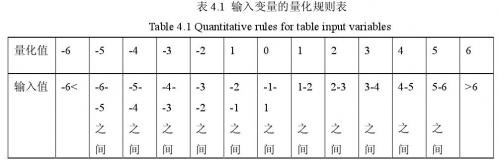
（3）知识库输入、输出变量的模糊子集选取为：负大、负中、负小、零、正小、正中、正大（NB、NM、NS、ZO、PS、PM、PB），确定了模糊语言变量之后，接下来选择各变量的隶属函数。一般地，隶属函数有三角形、高斯型、梯形等。对于隶属函数的选择，目前也没有完整的定论可以说明针对哪种控制对象使用何种隶属函数是最优的。因此，选择隶属函数一般都是根据经验或从计算简便上考虑。误差和误差变化率输入、PID参数的输出变量的隶属函数均选取为三角形隶属函数，统一使用下面隶属函数图4.8.