chain and scattering parameters

Hallo,

the chain matrix of a simple series impedance network can be expressed
as
C=[ 1 , Z ; 0, 1 ]
translated into scattering parameters, we get
S=[ T21/T11 , T22- (T21 T12)/T11 ; 1/T11 , -T12/T11 ]
S=[ 0 , 1 ; 1 , - Z ]

Does anybody see the mistake. The series impedance should be
symmetric. Here we have S11=0, S22=-Z, S21=S12=1.

Thanks for your comments.

Hello
the formula which you use seems to be wrong just because it doesn't include characteristic impedance Zo:)
Try to find the right one.

If there is a scattering matrix referenced to Z0 at all ports,
the corresponding chain matrix is also referenced to Z0 at all ports.

---------- Post added at 17:45 ---------- Previous post was at 17:33 ----------

Anyway, there seems to be a mistake. The formula I use for years should read like this:
S=[ T12/T22 , T11- (T12 T21)/T22 ; 1/T22 , -T21/T22 ]
This way the following C, S matrices correspond:
C=[ 1 , Z ; 0, 1 ]
S=[ Z , 1 ; 0 , 0]

The picture shows screenshots from two different books.

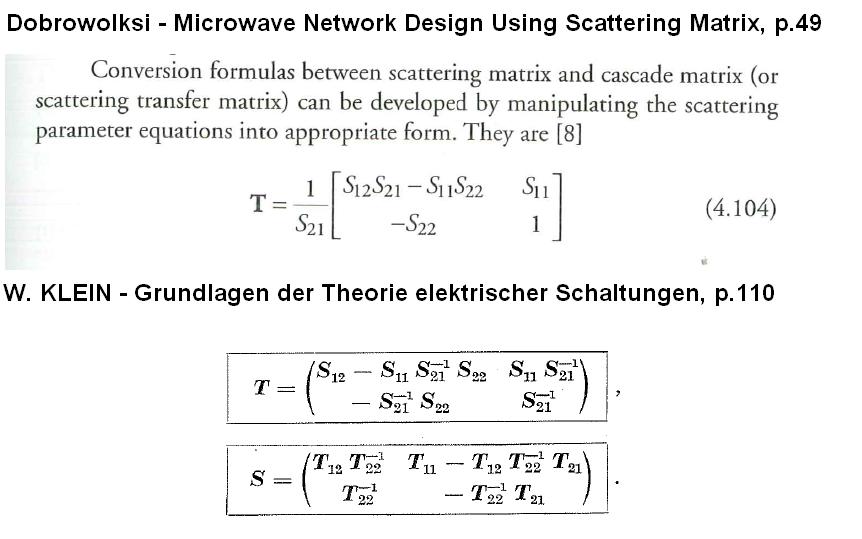
---> Well, I think
C=[ 1 , Z ; 0, 1 ]
may be valid for the so called ABCD matrix (voltage, current based formulation).
But it has to be wrong for chain matrix formulation.

The scattering parameters of simple series impedance network should be

S11=S22=(Z/Z0)/(2+Z/Z0)
S21=S12=2/(2+Z/Z0)

Which gives a different chain matrix ...

Actually i'm not familiar with T-parameters very well. ABCD parameters of serial impedance A=1 B=Z C=0 and D=1 and if you use the following conversion rules

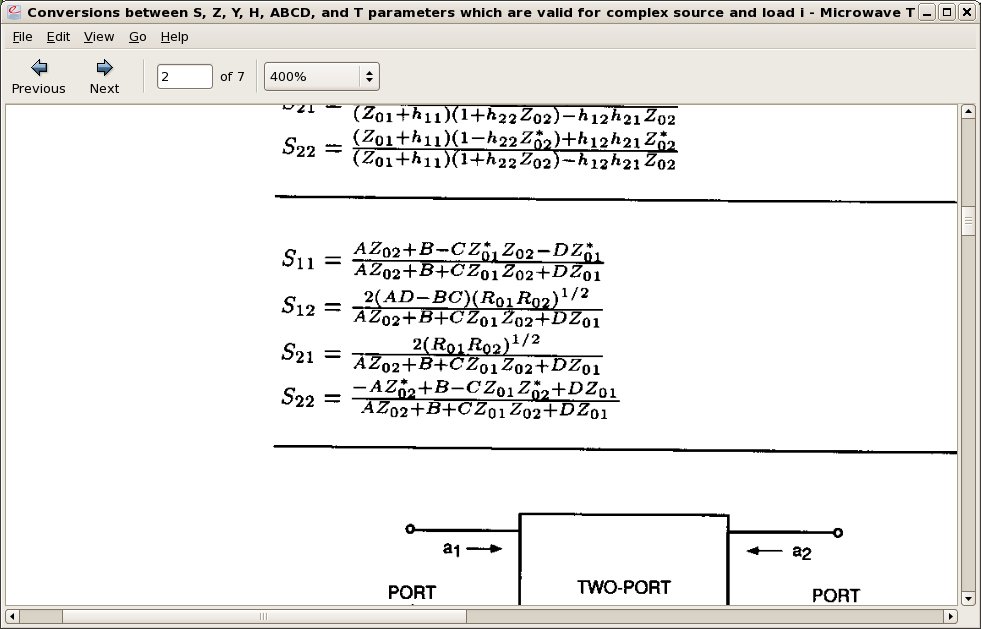
the answer seems to be right
S11=S22=Z/(2Z0+Z)
S21=S12=2Z0/(2Z0+Z)
Regards.

Ok, problem solved. Thanks ...