Problem calculating complex impedance

Hey guys,

I'm doing a project on RF and I ran into a problem. I hope you can take the time to try and answer some of my questions.
I build a 15dBi Yagi antenna for wifi purposes and I have done some measurements which include plotting the S11. But now I want to turn these values into complex impedance (read: Zin). The formula to do this is: Zin = [(1 + S11) / (1 - S11)] * Z0, in which Z0 is 50 ohm. Now, as I tried this formula out on my theoretical values in my 4Nec2 design I found something strange. If I'd take a theoretical S11 value at a certain frequency it wouldn't match the theoretical Zin at the same frequency. Example:

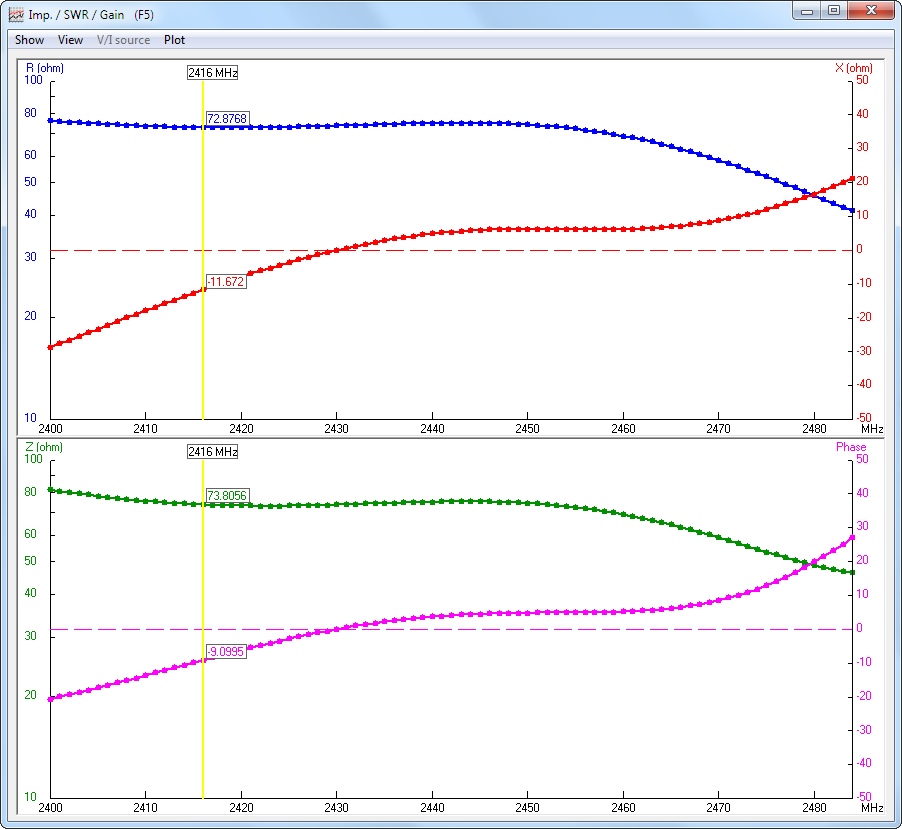
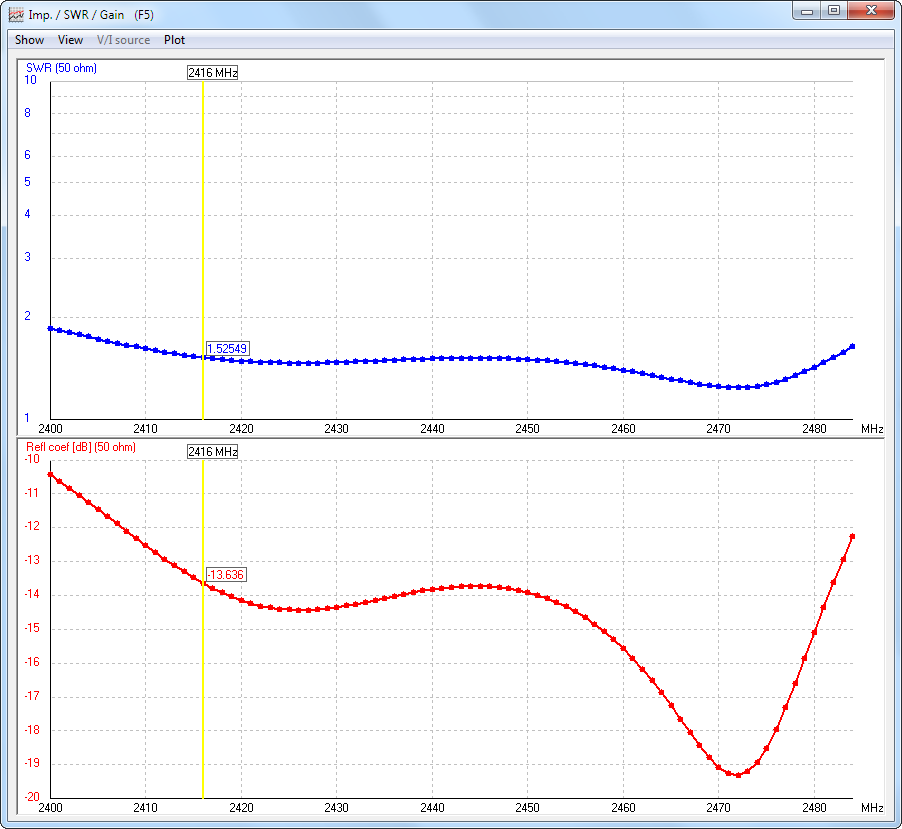
S11 = -13.6 dB @2416MHz
Z0 = 50 ohm
gives => Zin = -43.2 ohm

whilst the theoretic value of Zin is 73.8 ohm. (see attachments)

What am I doing wrong here? Perhaps the Refl. Coef =/= S11?

I would be really grateful if you'd take the time to answer my question.

Greetings from Holland

Woops! I think something went wrong uploading the attachments!

S11 is not the same type of parameter as return loss or VSWR. Return loss and vswr are scalar quantities. S11 is a vector quantity, containing a magnitude AND a phase, or if you prefer to think another way--it has a real and imaginary part. You equation assumes you will enter the vector value for S11. Since you entered only a magnitude....the answer will certainly be wrong.

If it were me, I would take your return loss and phase info, convert it to real [S11] and IM [S11], and then do the complex division, like this:
division of complex numbers

The answer will probably show that the impedance is a complex quantity also, i.e. not just resistive.

Thanks for reply. I didn't know the S11 had to be a complex value. I'll take a look, and see if I have the associated phase info. But wouldn't it be easier to just use Pythagoras to determine the value of the vector and use it in the formula I stated in the thread earlier?

Again, thanks a lot for taking the time to respond.

I am pretty sure Pythagoras did not have access to a network analyzer. How do you propose to use his formula to go from a scalar to a vector?

You can go the other way around...if you have a real and imaginary part, you can square them, sum them, then take the square root. The answer is the MAGNITUDE. But once again, you have thrown away the phase info needed for your ZIN calculaton.

S11 is a vector with a magnitude and a phase. A real part and an imaginary part. The magnitude equals the power return (in my example -13.6). And let's say I have the phase info (I'm not sure if I have it, the file is on another computer). But lets say I have the phase info... I'd have a magnitude and a phase, a real part and an imaginary part, right? I can turn that into a vector. That vector being the S11 value in the formula.

I'm sorry but I don't think I get what you're saying, sadly. Can you please elaborate?

Thanks

You used S11 in dB that is absolutely wrong, you can not use these as in dB.

You must use it as complex variable in that formulae..

If you only want to verify the calculations of 4Nec2 and you don't have the phase information of S11 you could do the calculations the other way and calculate S11 from Zin. This will get you the real and the imaginary part of S11 (respectively the magnitude and the phase). (With this you could then again calculate the Zin and test if your calculations are correct)
For the formulas you can look for example at wikipedia: Reflection coefficient - Wikipedia, the free encyclopedia (but keep in mind this are all complex numbers!)

Thanks for your response. I do however have the phase in my .Nec file (see attachment). But please explain me this:
If I've got a S11 magnitude value (being the refl coef) and I've got the associated phase, I'd have a real and an imaginary part of the S11 right?
I could use Pythagoras' formula to calculate the vector of those two parts. The vector being the complex S11 value, ergo the value I need for my formula. Why doesn't this work?

Thanks for taking the time to help me!

edit: perhaps the phase (see attachments) is associated with the impedance. In this case I do not have the phase.

Reflection coef. and S11 are same. You know that how to calculate reflection coef, it is ref_coef=(zin-z0)/(zin+z0). You can find zin in terms of ref_coef. zin=z0*(1+ref_coef)/(1-ref_coef). There is nothing confusing.

Edit: Reflection coef. and S11 are same if all other ports see z0 because s parameters are defined under certain conditions.

Alright I got it. Turns out what I thought was the S11, actually is the return loss. So first you'd have to turn the RL into the S11 value. By doing:

S11 = 10 ^(RL/-20)

And then use the S11 in the formula:

S11 = (ZL - ZS) / (ZL + ZS)
in which ZL = impedance to load and ZS impedance to source. (ZS = 50 ohm).

Thanks for your help though!

A short note: The S11 and the return loss are the same. But they are often stated in dB:
S11dB = 20 * log(mag(S11)) and vice versa S11 = 10^(S11dB/20) - this is just the magnitude of S11!
For information about dB calculation you could look under Decibel - Wikipedia, the free encyclopedia