what does directivity stand for photodiode?
I get a question for "directivity" for the photodiode?
Below is the "directivity" for S2506 from hamamatsu.
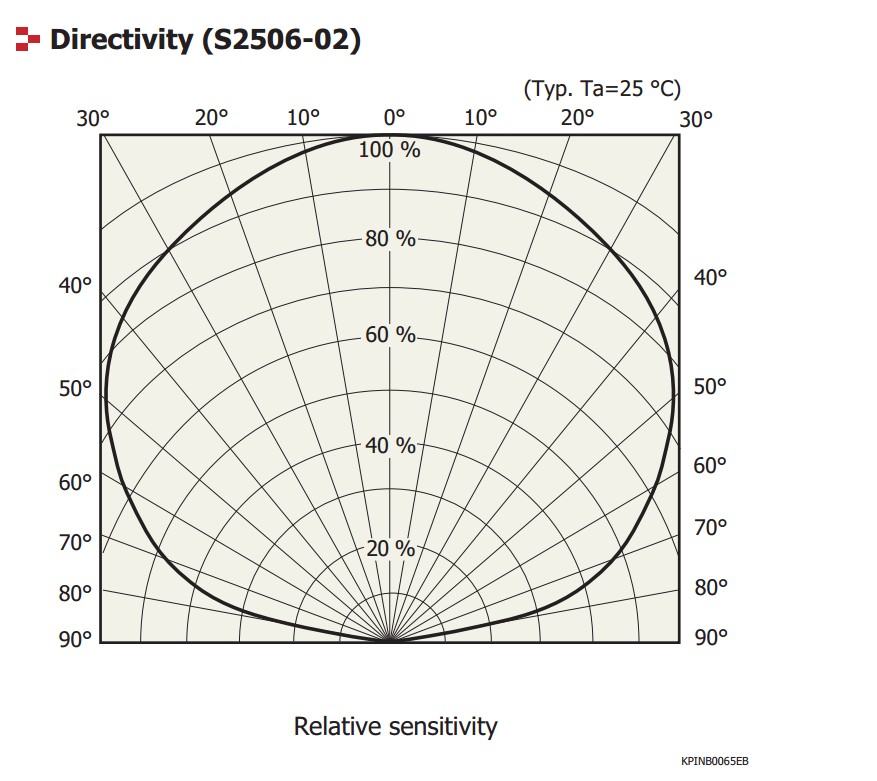
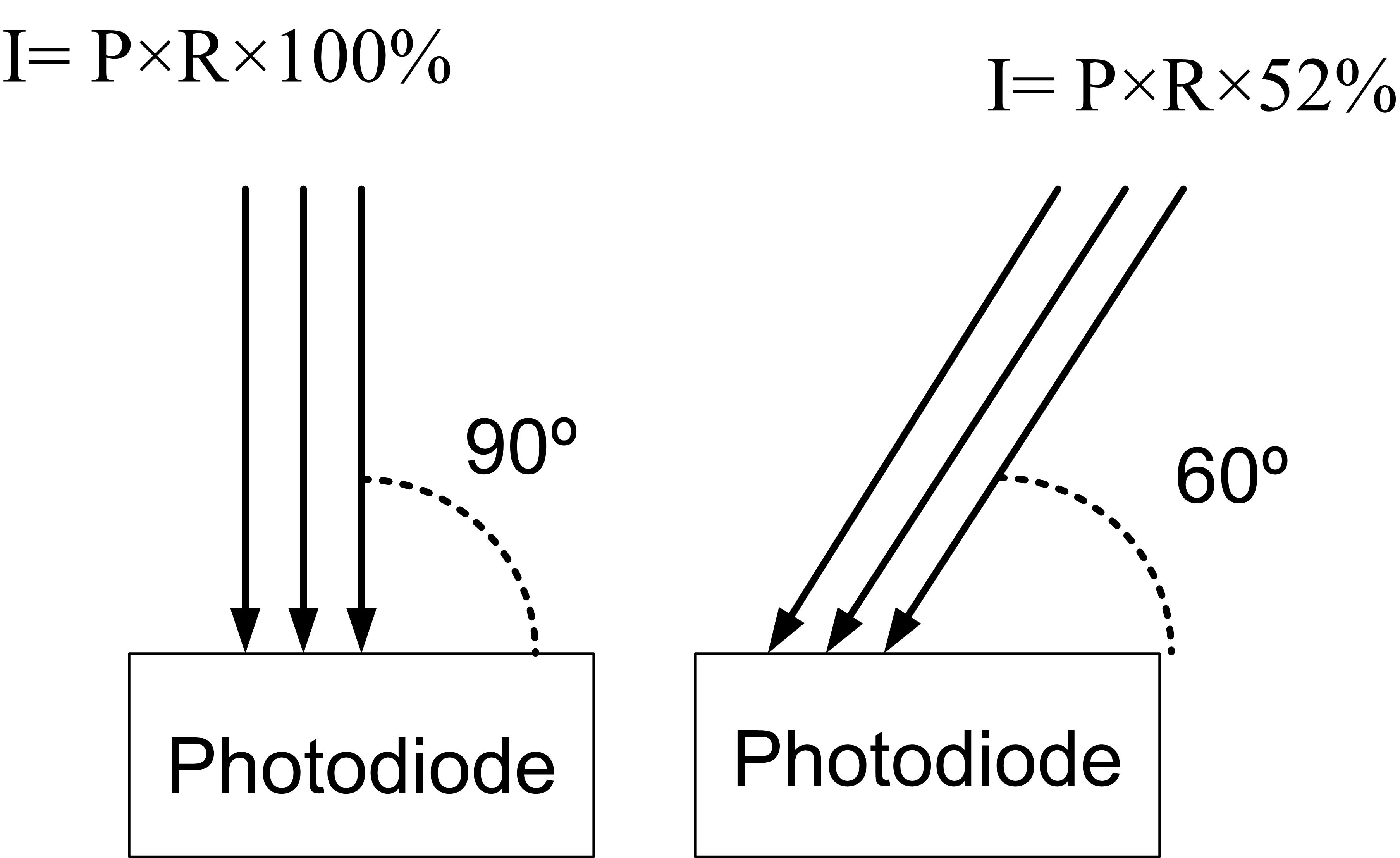
Does it mean when the light is incident to the photodiode Vertical. I= P*R , where I is the current, and R is responsivity , unit in A/W.
And when the light is incident at some angle, for example 60 degree. I= P*R * 52%?
Am I right?
I dont know what you mean by I=P*R. But I guess that you got the idea. The graph is a polar plot of relative sensitivity versus angle of incidence. Meaning that when the photodiode is pointed directly at the light source (zero degrees) it will have 100% sensitivity and at 60 degrees it will be closer to 60%. At 30 degrees you will get 90%.
and , do you know, why the incident angle will cause a decrease of the sensitivity?
Some photodiodes and other photo devices have integrated lenses, then is easy to guess why the sensitivity varies.
Here you can see the comparison between one with a flat window and another with a lens.
http://jp.hamamatsu.com/resources/pr...pin1010e02.pdf
The S2506 has no lens so I think it should be related with lower energy captured by the device. Pointing a flashlight to a wall at 90 degrees will give more illumination than doing so at 45 degrees and none if it is parallel. Because the same beam is spreading over a larger area.
Let's first remain the question in the photodiode without lens. ..
so I don't understand why "Pointing a flashlight to a wall at 90 degrees will give more illumination than doing so at 45 degrees" ?
because in my first picture, all 3 rays (or 3 photons) hit the surface of the photodiode, So. the current should be the same.
As already said by albert22, you have to consider the power density (incident power/area), that depends from the incident angle. When the rays are perpendicular to the surface, the power will be focused on a given area, but if you tilit the source this area will increase. If the rays are all parallel one each other, you can simply consider the triangle formed by the surface, the "last" ray and the line (or better the plane) normal to the rays. the surface will be the hypotenuse of the triangle, the the area now illuminated on the surface will be the original area (illuminated by perpendicular rays) divided by sin(alpha), where alpha is the angle between rays and surface. for alpha=45 deg. the surface will be rougly 40% more. This is why the summer is warmer than winter.
Thanks, however I am still confusing, why "tilit the source this area will increase"?
below is your triangle, and up is mine, should it be the same illuminating area no matter the angle the light incident ?

The idea is the following:
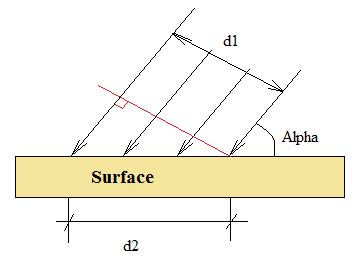
The red line represent the normal projection, its length is d1. On the surface instead the projection will have a length d2=d1/sin(alpha)
Get it ! and thank you so much.
