Powerful learning approach: reverse engineering of microwave circuits from internet.

In this thread i want to discuss microwave circuits from internet. It can be mixers, oscillators, filters, etc. - there are many amateur sites and tons of papers with design examples, that can be analyzed in many ways. So we can learn something new and check theory, even if somebody have no access to expensive measurement devices, such as network analyzers and spectrum analyzers. Using device parameters and other data given by authors, even layout photos, we can try to design the same device using our methods, software tools, and check how far our result differs from the original authors and discuss it. Additionnaly i want to recreate some of those circuits for lower frequency bands, to prove theory on practice. Maybe some students will get ideas about their final projects,etc.

I want to start from analyzing this paper: Quadruple-push oscillator (see preview available), then learn Octa-push oscillator. The good thing is that authors provide photos of their prototype boards, active device model and dielectric constant of laminate.

1. Starting from digging datasheet on active device:
Used FET transistor FHX35 (datasheet: www.qsl.net/n9zia/pdf/FHX35LG.pdf)
Frequency of oscillation: 8.95GHz. We can use S-parameters for 9GHz or interpolate between 8GHz and 9GHz. I will use 9GHz:
2. Obtaining millimeter lengths of microstrips.
Approximately lengths can be obtained using lead sizes of FHX35 transistor. Or we can use frequency, dielectric constant and size of microstrip resonator, but i prefer first way (see later why).
FHX35's width between leads (source to source or gate to drain) = 4.78mm
FHX35's diameter of ceramic part approximately = 1.78mm
Measuring size of this elements in pixels we can obtain scale coefficient and calculate lenghts of other parts:
Now we have approximate lenghts of some microstrips:
gate stub is 7.1mm, drain stub is 5.5mm, resonator side is 6.999=7mm.
Resonator full lenght is 7*4=28 [mm]

There is also short source stub, but it's configuration is unclear to me (short to ground only at one source lead). It will have effect on S-parameters of transistors, maybe it is inductive stub for increased instability. Anyways, we can try to add different inductance later to see if we can calculate the same Drain and Gate stub lenghts as in original design.

3. Trying to design the same microstrip layout using my little knowledge.
Dielectric constant Er of used laminate is 2.15.
I like to use online microstrip line calculator from this page: http://www1.sphere.ne.jp/i-lab/ilab/tool/ms_line_e.htm
Using this calculator, we obtain values:
effective Er = 1.879
lambda/4 = 6.08 mm
Using some formulas can
Here is first surprise: one-wavelength microstrip resonator length must be about 24.4mm long. If it is ring resonator shaped as square,
each side of it is about quater-wavelenght = 6.1mm
But in original design resonator lenght is about 28mm long, and quter-wavelength side of a square is 7mm.
Even if we calculate Er effective with 100 Ohm lines, quater-wave is 6.3mm, that is still far from 7mm.

Trying to do it another way. Resonator square size is about 82 pixels.
Resonant frequency is 8.95GHz
Er=2.15
Gate and drain stubs looks about 50 Ohm, and resonator line is thinner, maybe 25 Ohm.
Trying to get scale coefficient one more time:
Stubs:
Drain stub is 5.1mm, gate stub is 6.5mm.

4. Trying to calculate drain and gate stubs based on S-parameters of device and compare it with original design:
Stability coefficient is too high, because source stub not was taken into account:
I choosed reflection coefficients this way:

Gate and drain impedances can be realized using open stubs:

In original design drain stub is 5.1mm, gate stub is 6.5mm.
Ours: 6.3mm and 7.29mm.

After adding inductance stub, k becomed <0. But gate and drain stubs becomed longer than in original design: both> 10mm.

I am going to continue to analyze this circuit in next posts. Next logical step is to build script for searching reflection coefficients for original stub lenghts.

I found error in typing S12 S-parameters, it must be:

Results of my calculations vs original design:
gate stub = 7.3mm VS 6.5mm
drain stub = 6.3mm VS 5.1mm

Difference is about 1mm for each stub. Assuming source stub influence on S-parameters did not taken into account and pixel measurement erros, it is not so far from original result.

Let's try to add source stub. We can't see how microstrip goes under the FET. It can be whole quarter-wave microstrip line with short to GND on one side, or two separate stubs with one grounded. As separate grounded stub have inductive behaviour, i guess it is. Also it can be capacitive stubs? After playing with source stub it becomed obvious, that it's influence on gate and drain stub made them ever bigger, and far from original design. I am going to see original gate stub impedance on smith chart and see where it is:

gate stub is 6.5mm,
electrical length: 90*OriginalGateStub/pcbquarterwave = 91.8deg.
Gate impedance is 0+1.5i. On smith chart it is point DP1, near inside part of unstable input circle:

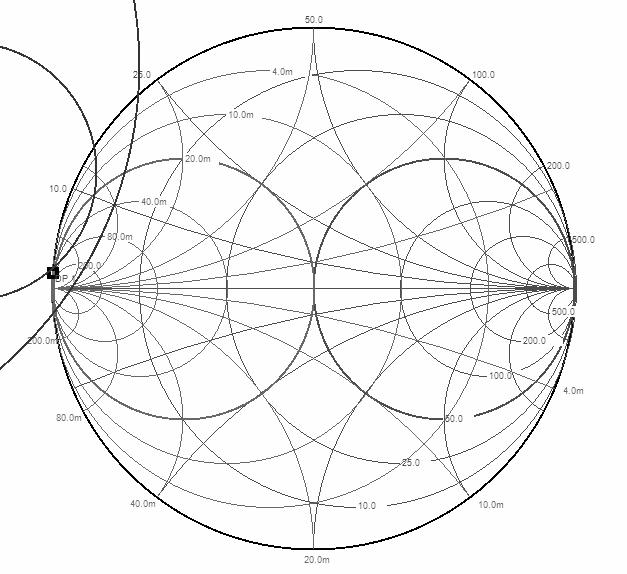
This point is almost the same, that was choosen in our calculations. Trying to use original gate stub reflection and recalculate drain stub gives no improvement. As we have enough freedom in choosing reflection coefficients, stub lenght variations are not so important. I think such scheme can be reproduced for lower frequency doubler/quadrupler this way: make negative resistance scheme: calculate reflection coefficients, add matching stubs for gate and drain (only match phase, so no additional stubs). DC-couple two equal oscillators to ring resonator. Source is grounded, without additional stubs.