Characteristic impedances...

Hi.
What is the characteristc impedance of two 50Ω RG8 coaxial cables of the same lenght, connected in parallel ?

Hi Externet,

By parallel, do you mean the inner conductors are connected together, and the outer conductors are connected together? In this case, there is no coupling between the independent cables.

The characteristic impedance of each cable is derived from its geometric properties, typically in solving these problems we assume some applied voltage/current and solve for the series L' and shunt C' values, then use Z_0 = sqrt(L'/C').

In your question, there is effectively two L' and C' in parallel, meaning L'_total = L'/2 and C'_total = 2*C'. Inserting this into the above equation for characteristic impedance gives Z_0_total = sqrt(L'/(4*C'), or Z_0/2.

So, assuming that there is no coupling between the cables, the characteristic impedance is simply halved, as is the case with the impedance of ideal circuit elements (which are ideal because they don't couple).

Thanks PlanarMetamaterials.

Yes, both transmission lines having their center conductor joined only at both ends; and shield braids joined only at both ends of the two 50Ω transmission lines with their proper vinyl jackets intact, and separated by average 1 cm, or touching insulations.
If Zo is "/2" then would be 25 Ω, right ?
So they behave as resistors ?

Yes, with that setup the system will have a 25Ω characteristic impedance.

The characteristic impedance of the two in parallel is halved, yes, the same as two similar resistors would have their impedance halved. The actual resistance of the system will not be 25Ω.

Thanks. Then why two 50Ω transmission lines in 'series' RG8 + RG58 is not ~100Ω ?

The L' and C' quantities in my analysis are per-unit-length quantities. In other words, the characteristic impedance is affected by the cross-sectional profile of the system. Two cables in parallel will change this cross-section (from a system of one cable), two cables in series won't.

you can not, for cables longer than a short length, treat two parallel cables as modeled as a simple transmission line of lower characteristic impedance. it is way more complicated than that.

For instance, if you took two lines of 50 ohms and half wavelength long, an put them in parallel, you would find them making an excellent ring resonator.

sometimes two short lengths do behave that way. Say you have a filter that needs a shorted stub a quarterwave long and 10 ohm impedance. You can replace that stub with two independent stubs that were a more realizable 20 ohm characteristic impedance, and get nearly the same result. but you have to be careful in real life, if one stub were slightly longer than the other, a weird antiresonance can occur right in between the two resonant nulls, as Foster's reactance theorem predicts.

Can you elaborate what would happen in this specific case?

probably an insertion loss dip of a few db right at the resonant frequency. I will run some sims later and post what I find.

the power going down the line meets the two lines at a "T" junction, and evenly splits. it then travels down both lines, but meets another "T" junction. at that point the power recombines into one line going to the load...most of it going to the load, but a little from both of the parallel lines going back up the other line...basically to create havoc. something like triple travel ripple in a saw filter. lets see if I am right.

The two 50 ohms lines behave exactly like a single 25 ohms line, also regarding resonances. The "ring resonator" behaves identical to one line with open ends. Similarly, if you terminate both ends with 25 ohms, there will be no reflected waves.

If that were true, then these two circuits should have identical responses, but they do not.

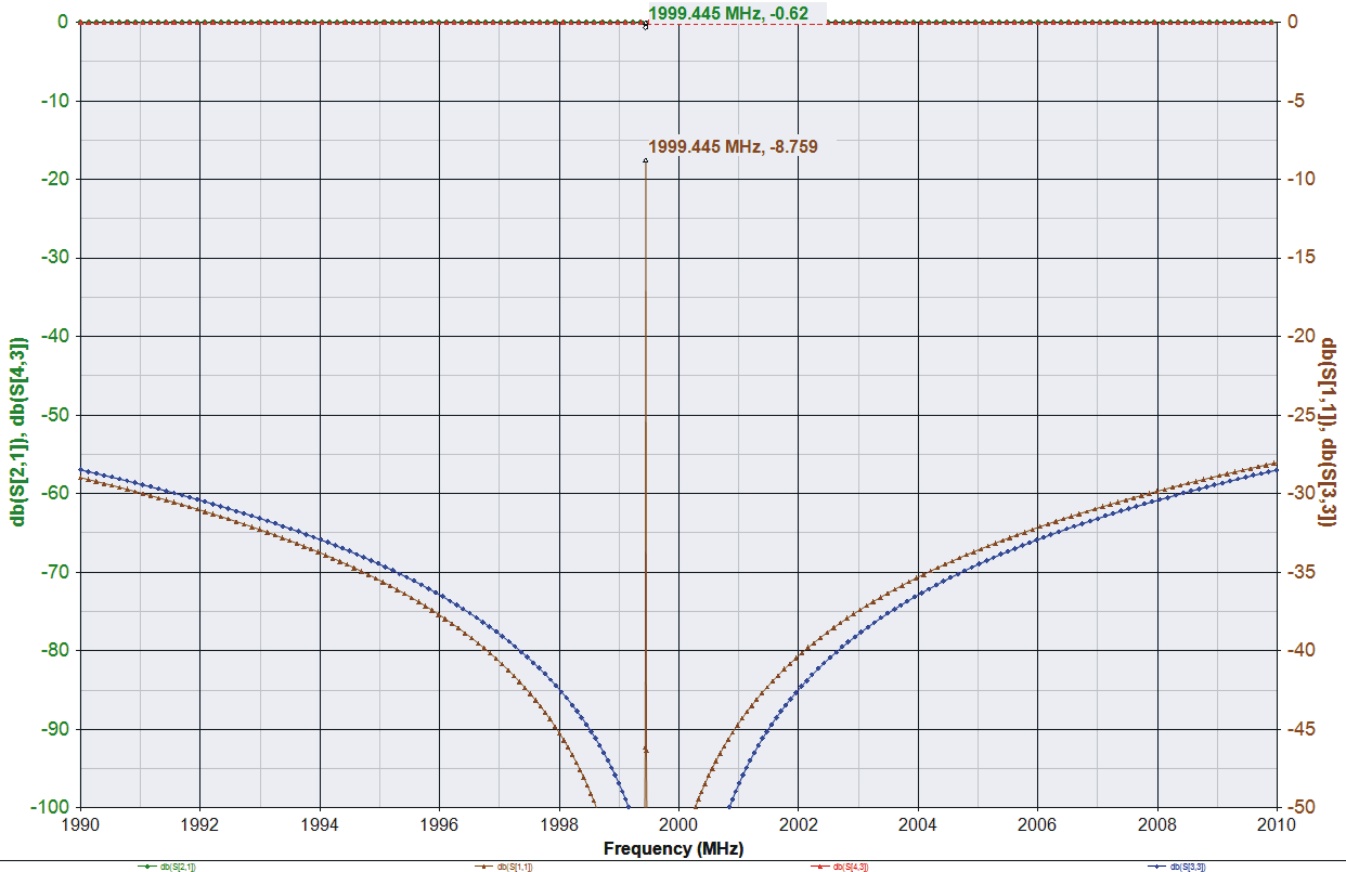
S11 is brown, S33 is blue

I tried this with a couple pieces of rigid coax at 150MHz a while back, and from what I could tell it acted just like a half wavelength section of 25ohm coax. Never saw any unusual peaks or dips.

its even more pronounced in a bandstop type filter, where you can have a tiny passband midband!

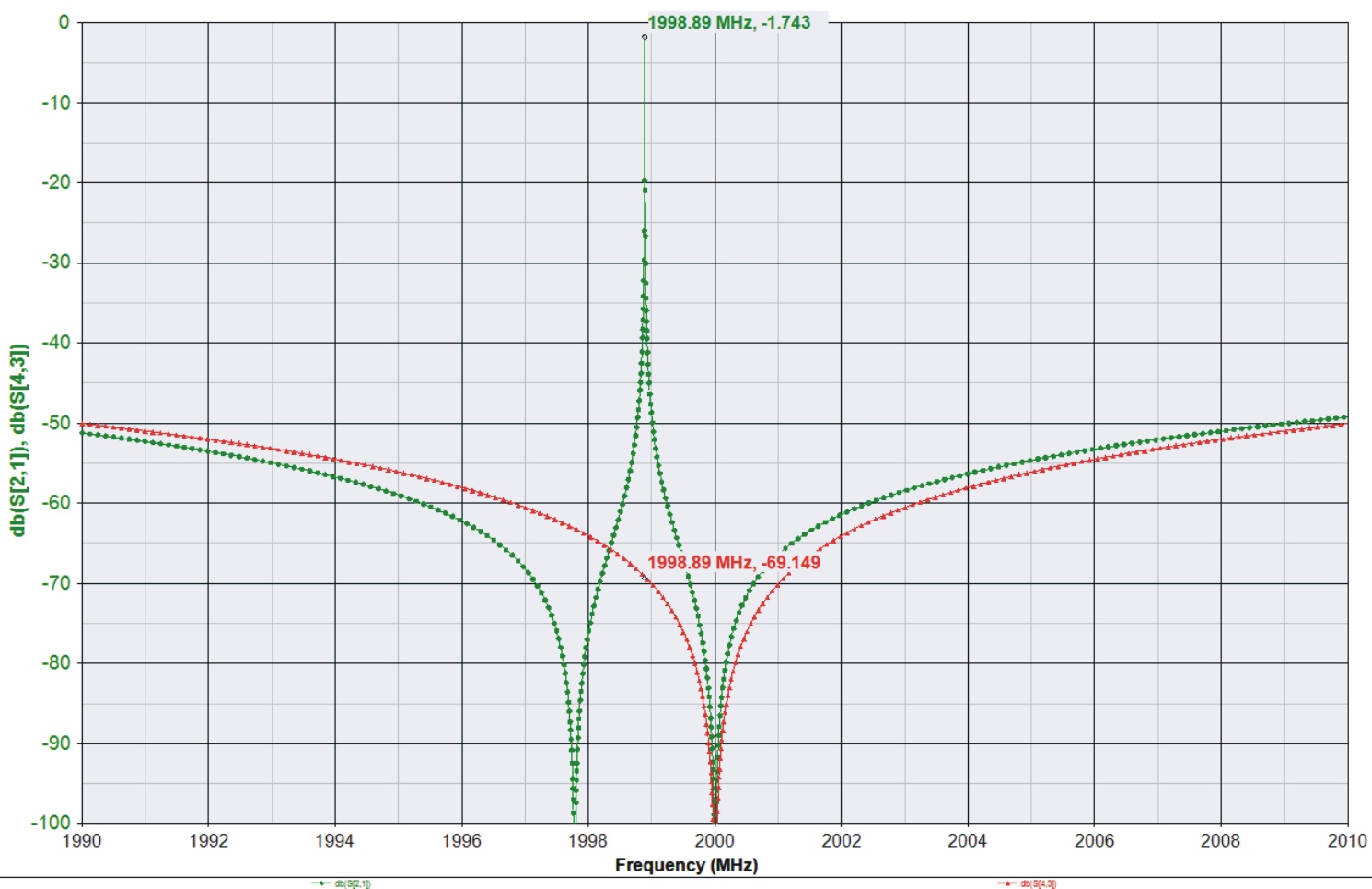
S[2,1] is green,
S[4,3] is red.

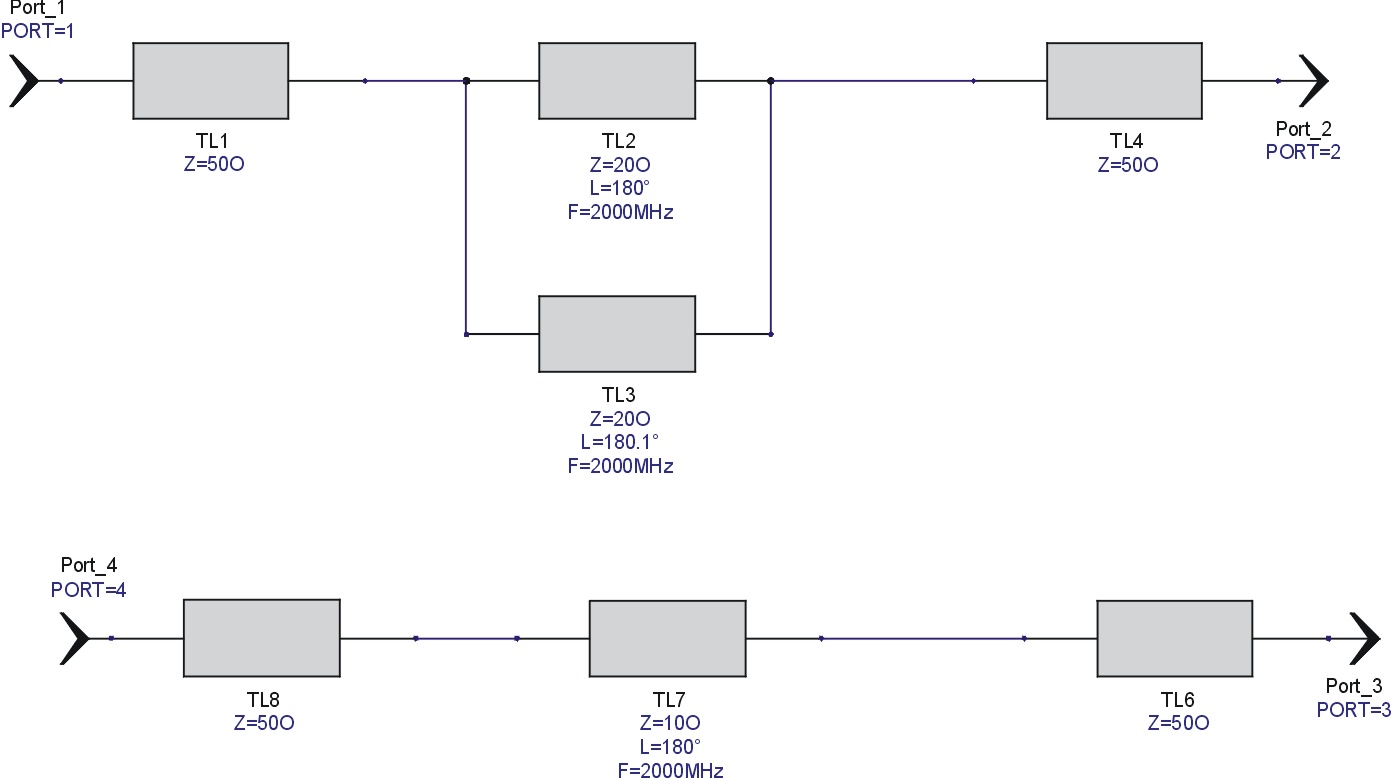
sorry, just realized you can not read the schematic...damned computers! the two stubs are 90 degrees at 2 GHz and 90.1 degrees at 2 GHz, both 20 ohm characteristic impedance, in the top circuit
the bottom circuit is just a single stub, 90 degrees at 2 GHz, 10 ohm characteristic impedance.

Obviously, the two circuits have VERY different responses.
The devil is in the details.

I ran into this once trying to improve the grounding of an active device, by paralleling a ground via with an open circuited stub. I eventually figured out that fosters reactance theory predicts an glitch at midband, since the ground of one circuit causes a zero impedance, then the impedance has to move around the smith chart as frequency increases, so it can not stay at zero ohms, but has to go thru the open circuit point before becoming a short circuit again. I hope I am explaining this well enough.



you have to look closely



I often wondered if one could use the bandstop filter with two nearly identical stubs to form a super narrowband bandpass filter instead. Kind of violating the laws of physics for the loaded Q"s of the two stubs? might make a good resonator for an oscillator too.

The "antiresonance" peaks are obviously there. Your simulation shows that rather small length differences matter if paralled transmission lines would be used in a TL resonator. Similarly, if you are making a matched transmission line system e.g. 25 ohm source, two parallel 50 ohm lines, 25 ohm load, small length differences are causing s21 notches. They definitely matter if a small band signals hits the resonances.

My "indentical behaviour" claim is only valid for the ideal equal length case.

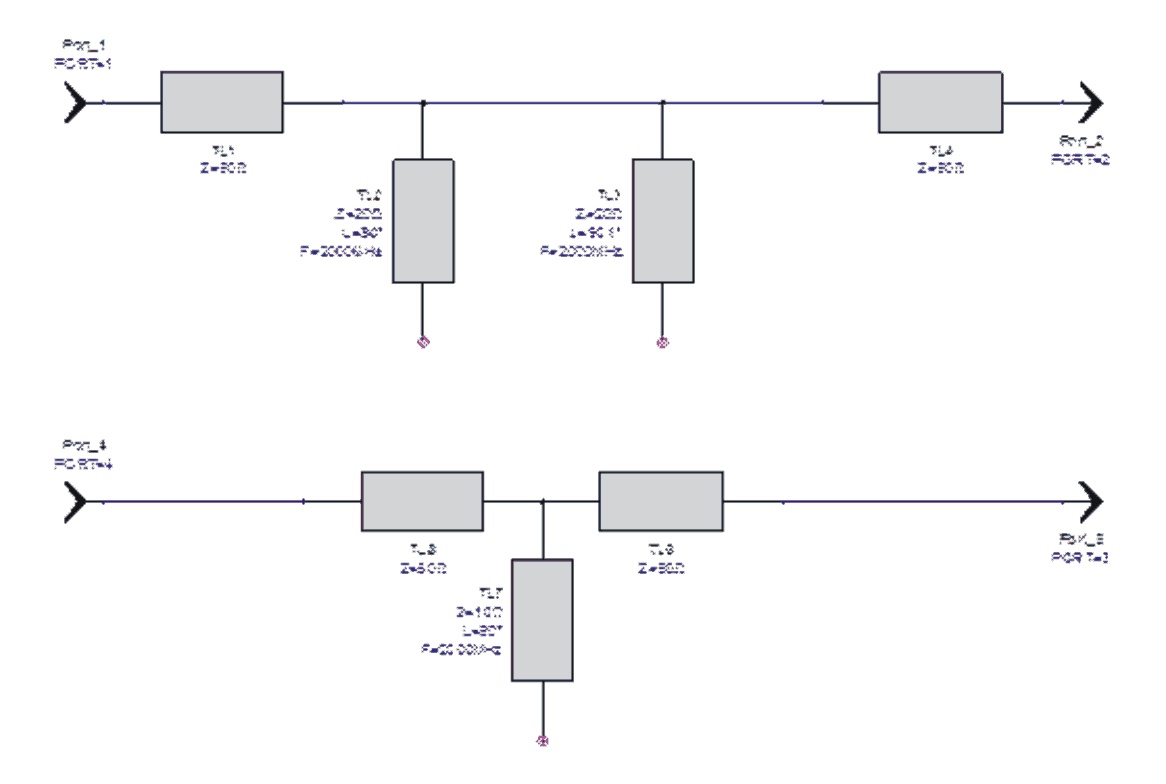
This is a different case, because you have connected the two lines only on one end. If you connect both lines at both ends, you will notice that the spike disappears.

No. You get different behaviour but still resonances as soon as both transmission lines have a small length difference. You can check with the simple setup proposed in my previous post.

so, you are saying if you have identical line lengths, like to the same micron in length, and no other non symmetrical parasitics, you can do this! sounds like a very useful design tool to me! lol



maybe there is a language problem, are you saying to take the two open circuited stubs, which are physically different end point locations, and try to connect them together? how would you do that in microstrip? typically you would lay the two stubs out on opposite sides of the main line so you would not have a parasitic coupled line.

Sure. What I did was just an ideal nodal connection at schematic level. Not realistic, but closer to the topic discussed here: parallel lines that are connected on both ends.

But anyway, after creating a setup like FvM suggested, I can see the issue. I was wondering how real this effect is if we include realistic line losses, but it's there. There is an issue when the line length is around lambda/2 or multiples of that.

It"s quite common, but you have pointed out the limitation: lambda/2 length must be avoided. Thanks for that insight!