第33章 实数FFT的逆变换实现

    本章主要讲解实数FFT的逆变换实现。

    本章节使用的复数FFT函数来自ARM官方库的TransformFunctions部分

    33.1 实数FFT的逆变换实现

    33.2 总结

33.1  实数FFT的逆变换实现

    本小节主要讲解实数FFT的逆变换实现，通过函数arm_cfft_f32实现浮点数的逆变换。

函数定义如下：

void arm_rfft_fast_f32(

arm_rfft_fast_instance_f32 * S,

float32_t * p, float32_t * pOut,

uint8_t ifftFlag)

参数定义：

[in] *S          points to anarm_rfft_fast_instance_f32 structure.

[in] *p          points to the inputbuffer.

[in] *pOut      points to the outputbuffer.

[in] ifftFlag     RFFT if flag is 0,RIFFT if flag is 1

注意事项：

结构arm_rfft_fast_instance_f32的定义如下（在文件arm_math.h文件）：

typedef struct

{

   arm_cfft_instance_f32 Sint;     /**< Internal CFFT structure. */

   uint16_t fftLenRFFT;            /**<length of the real sequence */

       float32_t* pTwiddleRFFT;          /**< Twiddle factors real stage  */

} arm_rfft_fast_instance_f32 ;

    下面通过函数arm_rfft_f32计算一个正弦波的FFT，然后再使用函数arm_rfft_f32做FFT逆变换，并使用 Matlab计算变换前后的结果对比。

1. /*
   
2. *********************************************************************************************************
   
3. *    函 数 名: arm_rfft_fast_f32_app
   
4. *    功能说明: 调用函数arm_rfft_fast_f32计算逆变换
   
5. *    形    参：无
   
6. *    返 回 值: 无
   
7. *********************************************************************************************************
   
8. */
   
9. static void arm_rfft_fast_f32_app(void)
   
10. {
    
11.      uint16_t i;
    
12.      arm_rfft_fast_instance_f32 S;
    
13.    
    
14.      /* 实数序列FFT长度 */
    
15.      fftSize = 1024;
    
16.      /* 正变换 */
    
17.     ifftFlag = 0;
    
18.    
    
19.      /* 初始化结构体S中的参数 */
    
20.      arm_rfft_fast_init_f32(&S, fftSize);
    
21.    
    
22.      /* 按照实部，虚部，实部，虚部..... 的顺序存储数据 */
    
23.      for(i=0; i<1024; i++)
    
24.      {
    
25.          /* 50Hz正弦波，采样率1KHz */
    
26.          testInput_f32_10khz[i] = 1.2f*arm_sin_f32(2*3.1415926f*50*i/1000)+1;
    
27.          printf("%f\r\n", testInput_f32_10khz[i]);
    
28.      }
    
29.    
    
30.      /* 1024点实序列快速FFT */
    
31.      arm_rfft_fast_f32(&S, testInput_f32_10khz, testOutput_f32_10khz, ifftFlag);
    
32.    
    
33.      /* 逆变换 */
    
34.     ifftFlag = 1;
    
35.    
    
36.      /* 1024点实序列快速FFT */
    
37.      arm_rfft_fast_f32(&S, testOutput_f32_10khz, testInput_f32_10khz, ifftFlag);
    
38.    
    
39.      printf("****************************分割线**********************************\r\n");
    
40.    
    
41.      /* 串口打印求解的模值 */
    
42.      for(i=0; i<fftSize; i++)
    
43.      {
    
44.          printf("%f\r\n", testInput_f32_10khz[i]);
    
45.      }
    
46. 
    
47. }

运行如上函数可以通过串口打印出原始正弦波和经过RFFT，RIFFT的正弦波，下面我们就通过Matlab对比变换前和变换后的波形。

    对比前需要先将串口打印出的两组数据加载到Matlab中，并给原始正弦波起名signal，变换后的数组起名sampledata，加载方法在前面的教程中已经讲解过，这里不做赘述了。Matlab中运行的代码如下：

1. Fs = 1000;                  % 采样率
   
2. N  = 1024;                 % 采样点数
   
3. n  = 0:N-1;                 % 采样序列
   
4. f = n * Fs / N;               %真实的频率
   
5. 
   
6. subplot(2,1,1);
   
7. plot(f,  signal);      %绘制原始信号
   
8. title('原始信号');
   
9. xlabel('时间');
   
10. ylabel('幅值');
    
11. 
    
12. subplot(2,1,2);
    
13. plot(f,  sampledata);    %绘制RFFT和RIFFT后的信号
    
14. title('RFFT和RIFFT后的信号');
    
15. xlabel('时间');
    
16. ylabel('幅值');

Matlab运行的结果如下：

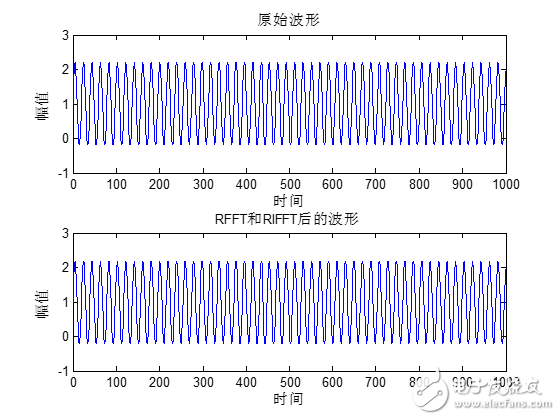
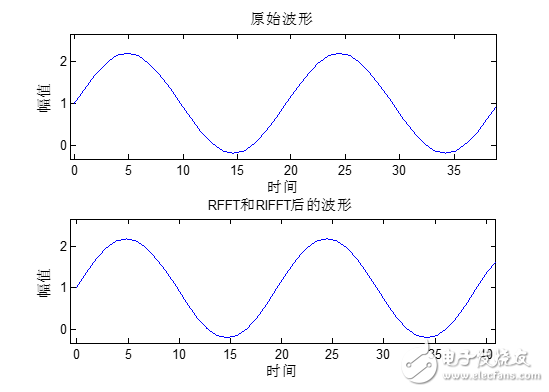
波形前端部分：

波形后端部分：

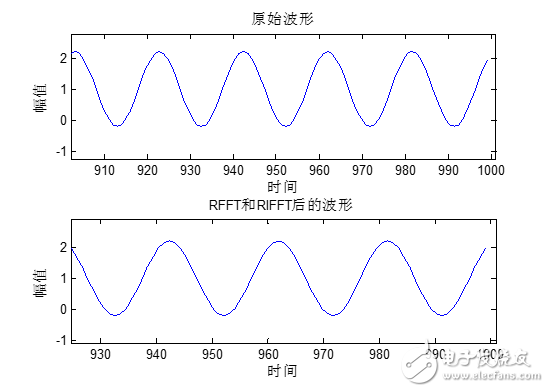
从上面的对比结果中可以看出，函数arm_rfft_fast_f32计算前后的正弦波基本是一致的。

33.2  总结        本章节内容较少，主要验证了函数arm_rfft_fast_f32正变换和逆变换，有兴趣的可以验证Q31和Q15两种数据类型的正变换和逆变换。