What is the cutoff frequency of the capacitively loaded Transmission line
In various books it is given that the cutoff frequency should be fc=1/(pi*sqrt(Ltl(Ctl+C/l))) but I don't see the same when I simulated. Thanks in advance.
Generally wrong, although I don't know what book you read.
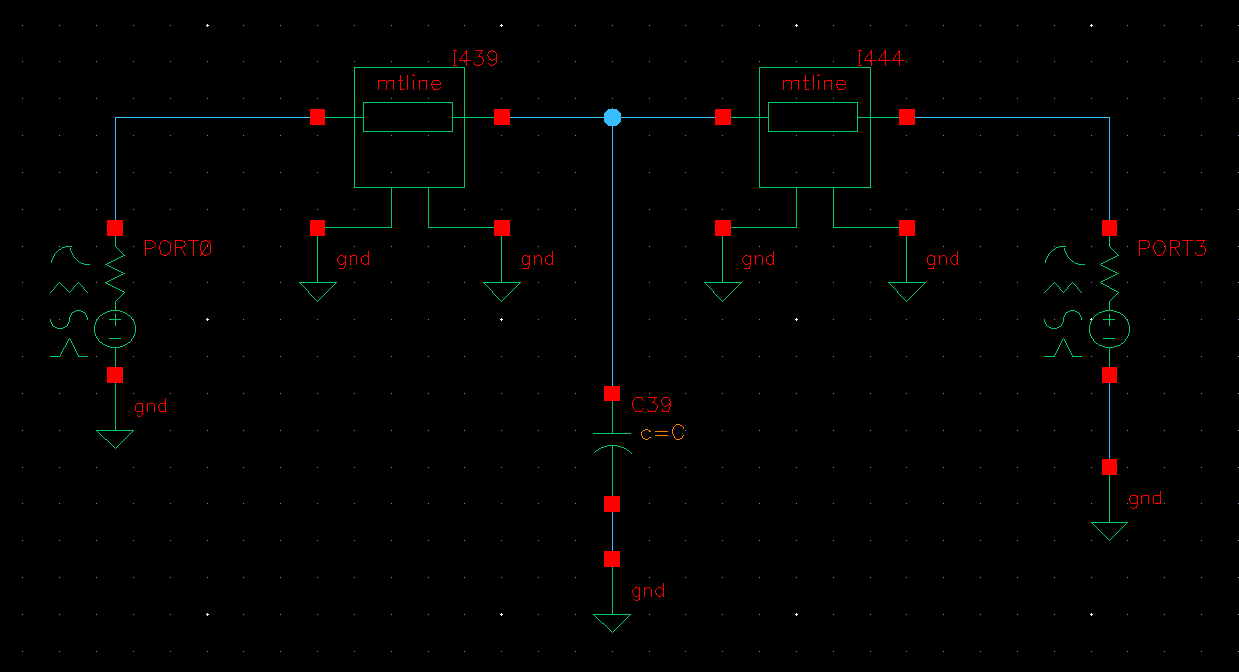
Your circuit is well-known capacitive discontinuity in uniform line.
What value do you set for reference impedance of ports ?
50 ohm in both ports
That's probably for an infinite cascade of embedded capacitors. I'm not sure how well one capacitor would reproduce this result. I would recommend to try additional periods and see of anything changes.
So large mismatch at port, although I don't know what you set for "mtline".
What quantity do you see in simulation ?
If mtline is setup as an ideal 50 ohm transmission line, the answer is very simple and you should be able to derive it yourself. Just a first order low pass with tau = c*Z0/2.
I used an RLGC file and the Z0 for line is more than 50 ohm
What quantity do you see in simulation ?
I see cutoff Frequency of 119.43 GHz in simulation
No.
What quantity do you see to evaluate cutoff Frequency in your EDA Tool Play ?
I check S21.
You must not use S-parameter, since you can not understand RF and very basic things at all.
https://www.edaboard.com/showthread.php?385709#2
https://www.edaboard.com/showthread.php?385709#7
What happens if the Line is not 50 ohm. is the same equation applicable?
Surely not.You get reflections at the ports, the line length also matters, and the frequency characteristic is no longer monotone. Theres's no simple cutoff frequency formula applicable.
Then when to use this formula fc=1/(pi*sqrt(Ltl(Ctl+C/l)))? which scenarios, line with infinite length ?
If the port impedances are 50 ohm (i.e, in matched condition) voltage gain is equal to power gain (S21). When the circuit is Linear, Pout(dBm)= S21(dB)+Pin(dBm). So it doesn't matter which one I am looking at, all should give same cut off frequency.
An example of Zline > Zport is shown below. How do you design cut-off frequency in this case?
I would consider the -3 dB point as the cutoff frequency. And as you mentioned there is no simple equation to calculate it.
