Problems with Stationary Current Solver in EM Studio 2008

Anyone here have experience with this solver?

I tried to simulate what I thought was a simple problem: a simple electrolysis cell comprising two cylindrical graphite rods immersed in a cylindrical beaker of water.

The hex mesh setting gave me two warnings:

1) All PEC regions are linked to source definitions. This problem is
overdetermined and leads to a singular conductance matrix.

2) Inaccurate J-field contains significant current divergences.
Please increase solver accuracy.

Yet there was no PEC material in the simulation, and the second warning always appeared, regardless of solver accuracy setting.

Surprisingly however, the solver did claim to finish "successfully", and the current values associated with the two current ports (one on each graphite electrode) were essentially equal.

Then, for purposes of comparison, I tried the tet mesh setting. Again, surprisingly, there were no warnings, yet the current values were obviously wrong (the values at the respective ports were unequal by a factor of almost 4).

I wonder what's going on here? It almost reminds me of the simple static magnetic field problems that EM Studio seems to be incapable of solving.

Hello,

Interesting problem.

not that i have many experience with it, but how did you try to model this structure, and what kind of materials did you use?

I'm doing some experiments with electrolysis and electroplating. I wanted to see what the plating current uniformity would be for a few different (non-optimum) electrode geometries.

I also wanted to be able to determine what the conductivity of a given solution would be by measuring the resistance I get in a cell of known geometry.

So I started with a simple case: two cylinders (electrodes) immersed in a third cylinder (electrolyte). Since I'm interested in plating a diamond-like-carbon (DLC)layer, and the electrolyte has a low conductivity, I think it's ok to use PEC material for the two electrodes and just assign a potential to each. And I used water as the electrolyte.

But in my experience CST has a long-standing problem and that problem has emerged again here. Every time a have a symmetrical problem geometry, I end up with asymmetrical field results. In this case the current density on each electrode should be the same within reason, but it's not, it's off by 30% or so as I see it.

Maybe you can try it? Just use the Efield solver with two cylindrical electrodes in vacuum. Set one at 10V and one at -10 volts and look at the resultant Efield on a 2D plane perpendicular to the longitudinal axes of the electrodes. If your results are like mine you'll see that the symmetry of the fields are way off.

My very simple model,

cyl1: vacuum, r=100mm, h=150mm
el1: pec, r=20mm, (x,y)=(50,0), h=150mm
el2: pec, r=20mm, (x,y)=(-50,0), h=150mm
all boundaries open,
V1=1, V2=-1
100.000 meshcells

I do a simple Es solve. Except for some little anomalies on the surface of the cylinders, the static voltage plot and the electric field energy plot seem fairly symmetrical. I defined no symmetry planes.

On the other hand though, when I try to simulate the electric field of a simple pin over a pec plane, the resulting e-field on the tip of the needle is strongly dependant on the mesh-density (obviously). Maybe your problem is a mesh issue?

Added after 18 minutes:

By slightly rearranging the above problem, I set the two cylinders as graphite (i add a small PEC cap on top of them) and set the body as default salt water.

I run the J solver and the currents and electric fields seem fairly uniform to me.

Originally, the current density plot I got was very jagged near the electrode surfaces (the place I'm interested in), and when using the cursor to readout the values, it was very asymmetrical, and changing with position in an unrealistic manner.

After experimenting with the mesh settings, I was finally able to get a more reasonable result (although it could still be better, IMO).

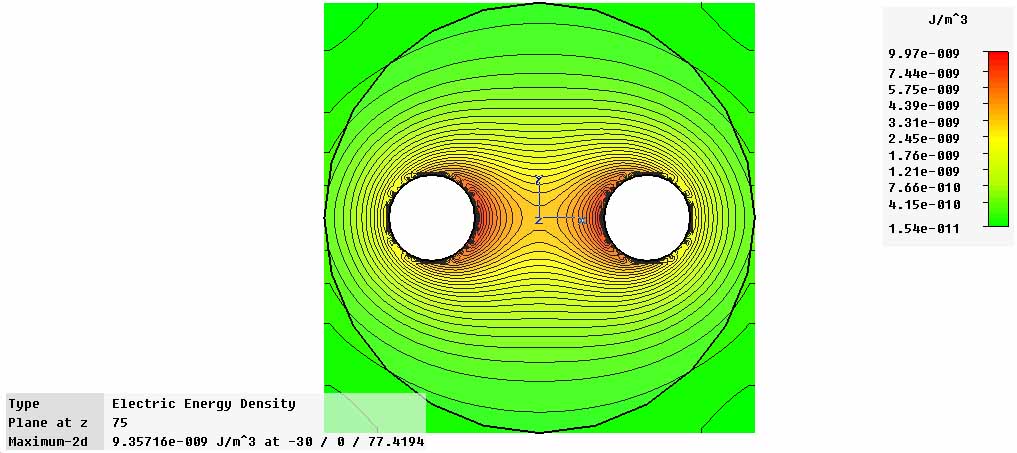
Anyway, I took your problem and switched to the stationary current solver, changed the boundary conditions to "tangential", and this plot results.

[img][/img]

Note the jagged edges and some asymmetry of the plot near the electrodes (this is what I was getting only somewhat worse).

BTW using graphite electrodes with PEC "connections" seems to get rid of the error message (thanks for that idea), although for what I was interested in, it turns out to be somewhat advantageous to have the solver ignore the electrodes.