一个面试问题：overshot和frequency peaking 的关系

早上笔试的时候遇到一个问题，不太理解，求助一下大家。
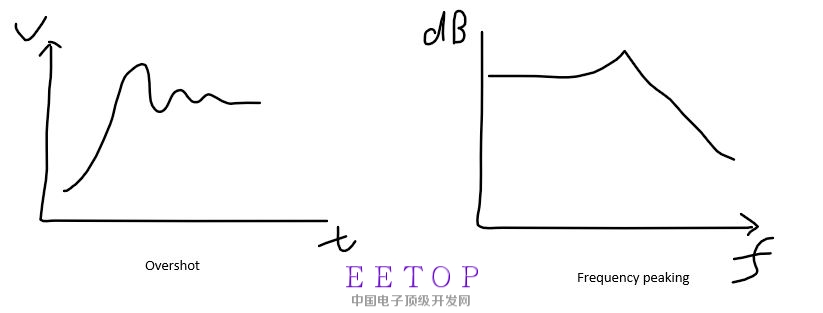
题目画了两个图，一个是时域的阶跃响应的overshot（过冲）现象，另一个是频域的frequency peaking的现象。
我大概画了下这连个图：

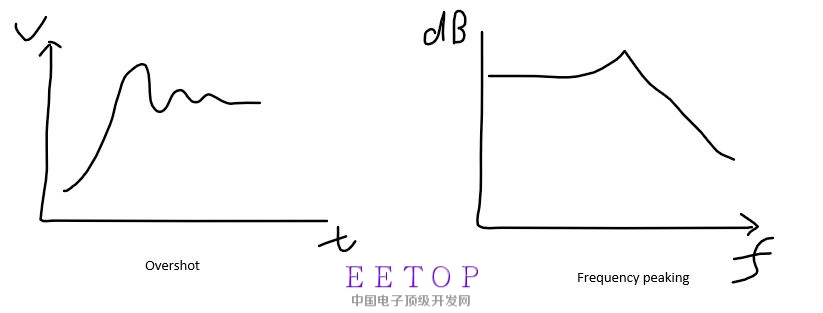
问题是（1）：overshot是否一定会导致频域的frequency peaking? 反过来frequency peaking 是否一定会导致时域的overshot。
（2）： 减小overshot可以怎么做；减小frequency peaking 可以怎么做?
感觉比较困惑，理解的不太清楚。

希望有大神能帮助解答这个问题，谢谢！

顶下。一个是相位余度问题，一个复数共轭极点引起的吧

相位裕度越小，过冲越明显，振铃越明显。

楼上正解！关于峰值的解释，Garder 的书里有说明。至于过冲，主要就是相位裕度的问题了。

一个是step response, 一个是频率响应。本质是一样的。
对于一个二阶系统，如果damping factor 0<zeta<1，是underdamped，有两个共轭根。系统还是稳定的，只是相位不够。这样step response就会出现overshoot, 频率响应就会有peaking.
减小都是同样的方法，让zeta >=1,这样就有两个实根，PM大。

谢谢回复！我想请问，阻尼因子zeta和反馈系统中的反馈因子之间是否有某种联系?
直观的来讲，反馈因子越大（即反馈越强），越容易不稳定，相位裕度越小，出现欠阻尼震荡的现象， 此时也有两个共轭的复数极点。
而反馈因子越小（反馈越弱），越容易稳定，相位裕度越大，出现阻尼收敛的现象。
和您描述的十分类似。

谢谢回复！
Razivi的书里给出了一个spice的仿真，那个电路的PM有65°，但仍然出现了overshot，他的解释是：”相位裕度这个概念很适合于处理小信号的设计。实际上，反馈放大器的大型号阶跃响应与图10.12（P291，中文版）不符。“
不知道您是怎样理解的?

關鍵在zeta呀~
推薦你去看signal and system的書，裡面對二階系統的數學描述會幫助你設計PLL。

大信号阶跃响应会改变dc点
频率响应是在某一dc点下计算的

有推荐的书和章节吗
我手头上有一本奥本海默的信号与系统

我的观点：
时域响应（左图）转化到频域，应该包括幅度特性（右图）和相频特性（未知）
该图的overshot 是由于PM小于65（或60）所致 ， frequency peaking 是由于极点所致，
问题（1）：overshot （存在极点）一定会导致频域的frequency peaking； 反过来frequency peaking 不一定会导致时域的overshot。因为 相频特性未知，PM未知。

（2）： 减小overshot，增大PM；frequency peaking很难减小，只能将frequency peaking推到不关心的高频去（或者零极点抵消）。如果硬要减小，那么电路的内部节点应尽量少，且为低阻抗结点。
个人观点

假如说只考虑纯极点系统，频域peak意味着存在复数极点对，相对应的时域响应一定会有ring。
时域有ring可能是因为两个实极点的系统相位裕度不够，频域上不见得会有peak.

赞同！

overshot是由于PM或GM不足导致的。
实极点或共轭极点peaking都有可能导致PM或GM不足。
在引入低频主极点的情况下，即使有高频peaking也能满足PM和GM。
减少overshoot一般就是想办法把极点分开，加大补偿电容降低主极点或减少晶体管尺寸来提高第二极点位置。有时尝试不同的电路架构也有机会的。
我感觉peaking和电路架构有很大关系，难改。
还有面试未必一定有标准答案。但你一定要有自信，能讲，即使错了也能博得好感。

学习学习

你没有说清楚这个频域图画的是什么传递函数的图。是开环传递函数的?是闭环传递函数的?如果是闭环传递函数的话，问题很简单，左右两图是对应关系，peaking越大，damping factor越小，overshoot越大。
如果是开环传递函数的话，问题就复杂了，左右两图没有绝对的对应关系。
谢谢。

稳定情况如何，除了PM，还要看GM。如果GM不够，同样存在稳定性问题。如果PM在60，GM比-10dB更负，跑阶跃还出现书上说的情况，我表示不服。

不错，不错

谢谢大家的回复，学习到很多，这几天恶补了下信号与系统，对这个问题有了比较全面的认识。这两者的确不应该是一种完全对应的关系。