请教两个计算电阻的问题
想计算一下附件图中的两种结构,从正方形框到中心的方形,从圆周到中心小圆的电阻,实际中外框和中心是两个电极。
1)中心方形边长为L,方形框的边长为M(宽度忽略不计),
2)小圆半径为R,圆周半径为S(宽度忽略不计)。
谢谢指教,有书里面讲过这种计算么,谢谢。
圆形的好算:
设大圆半径为R1,小圆半径为R2,平面高度为h,电导率为sigma,
取一同心圆半径为r, 在该圆上取一极小的扇区,展角为delta,
则该扇区的电阻为dr/(sigma*r*delta*h),
对r积分得到径向扇区电阻为ln(R1/R2)/(sigma*delta*h)
由于总共有2*Pi/delta个径向扇区,视为并联,
则所求电阻为ln(R1/R2)/(2*Pi*sigma*h)
直接取圆环的电阻然后沿半径积分就行了。D Δr / (2 \pi r h) 积分
方形的麻烦一些。但是可以等效成四个梯形电阻的并联。
梯形电阻似乎也没有现成的公式可以用。不过算起来也不难。
首先求梯形区域内的电场(电势)分布。稳恒电流下的电场分布与静电场的分布是相同的。电势都满足poisson 方程,对于你这个问题因为没有孤立电荷所以简化为 laplace 方程。边界条件就是梯形的上下边电位是确定的。比如你可以设长边的电位为0,短边的电位为 U。这个形状应该可以利用保角变换转换为长方形。之后就是分离变量法那一套解出场分布。
有了场分布再利用欧姆定律的微分形式就可以获得电流密度的分布。积分就是总的电流。之后电阻自然就求出来了。
我在考虑将梯形分解成一个矩形和两个直角三角形并联,然后四个梯形并联。这样解很容易,但是不知道有没有问题。尤其是在直角部分。
有问题的,因为电流分布不一定是直角
刚才吃饭时候想,分解成8个全等的直角梯形电阻并联是不是更合理一些。
这个分法应当可以
直接对梯形电阻积分:
取梯形中间一条线,长度为 l= t*L1+(1-t)L2,宽度为dt
电阻为dt/(l*h*sigma), 对t从0到1积分。
修正一下,宽度刚好是dl/2,因为45度角的关系。
这样积分就简化了。
电阻为dl/(2*l*h*sigma), l从L1到L2积分
这个方法不对,你不能保证你取得微元内电流密度是均匀的。微元内电流密度大的地方对电阻的贡献更大。举个极端的例子,你这个长条微元,如果只有一半有电流,另一半没电流,那对应的电阻就是你这样直接计算得到的电阻的一倍。当然这时极端情况,实际情况是这个长条中有些地方电流大,有些地方电流小。
有问题,不能这么分。因为电流会从矩形向三角型部分流动。所以不是并联关系。
分成直角梯形后还是面临相同的问题。你必须要计算场分布,没有捷径。
标准
.62
凭直觉,等势线应该是正方形的,所以电流密度在正方形的边上是均匀的。
如果俺的直觉没错的话。哈哈。
Matlab 算了一下电势分布。
明显等势线是弯的。。
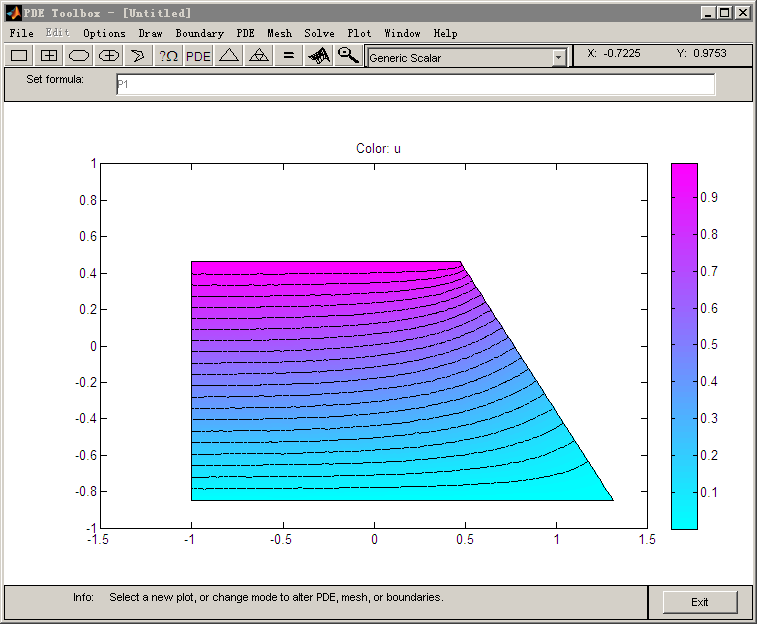
能算一下整个正方形的吗?
谢谢,看来正方形近似计算还是可以的,上面的推导算是个经验公式。
中心部分近似为圆形,靠近大正方形接近方形。用积分的方法得出来的值应该和实际值差不了太多。
其实 matlab 我用的不多。matlab 能做电路分析,但是肯定没有专业的电路分析软件用起来方便。
就好像用C/C++ 语言能不能做电路分析,当然是能,大多数电路分析软件都是用C/C++写的。但是很少有人直接用 C/C++ 来分析电路。。。
