PWM整流器的数学模型及控制策略

 1 引言

PWM整流器不仅可以控制AC/DC 变换性能，而且可实现网侧单位功率因数和正弦波电流控制，甚至能使电能双向传输[1],因此被广泛应用于功率因数补偿、高性能整流器、电能回馈、有源滤波等领域。整流器的输入端来自电网的三相电源，其相序a,b,c 在保证相位差120°的前提下只是一个相对量，而整流器算法中三相电源的相序涉及大量的数学变换以及PWM 波的输出，需在输入端定义。这样如果输入端接线错误，就不能实现算法功能。因此在不同的电网环境，必须先用仪器测量相序，再让整流器工作，这样的过程繁琐且容易出错。在此提出一种新的三相电源相序调整方法，有效地解决了上述问题。

2 PWM 整流器的数学模型及控制策略

2.1 PWM 整流器的基本结构

图1 示出三相VSR 主电路结构。可见，该电路由交流侧三相电感、三相全控桥、直流侧滤波电容组成。当VSR 正常工作时，通过PWM 波控制开关管的关断顺序，实现能量的双向传输。

桥臂上下两个功率开关管的导通是互补的，即上桥臂开关管导通时，对应的下桥臂功率开关管关断，其相应的逻辑开关函数为：


2.2 数学模型及控制策略

设定电网电压为：

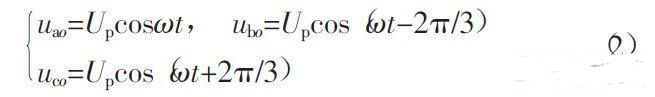
式中：uao,ubo,uco分别为交流侧a,b,c 与电源中点o 间的电压;Up为峰值电压。

由式(1)可得出三相静止坐标系下的开关函数数学模型为：

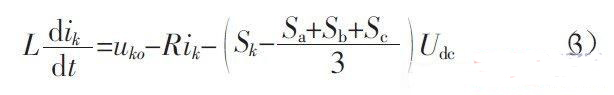
2 式中：ia,ib,ic为交流侧电流;Udc为直流侧的负载电压。

为判别相序，将三相电压转换成线电压。根据Clarke 变换，将a,b,c 坐标系转换为α，β 坐标系：

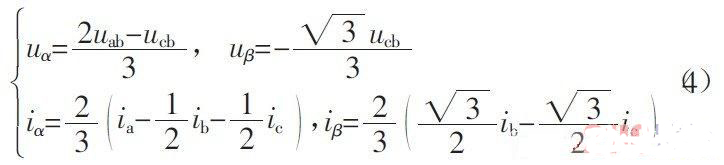
中：uab,ucb分别为线电压，且以b 相为参考点;uα,uβ,iα,iβ分别为α，β 坐标系中的电压和电流。
根据Park 变换，将α，β 坐标系转换为两相旋转d,q 坐标系：

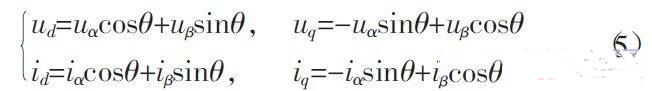
式中：ud,uq,id,iq分别为d,q 坐标系中的电压和电流;θ=2πft,f 为电网频率，0≤t≤Tuα,Tuα为uα的周期。
经过以上变换后，在d,q 坐标系中的三相电压型PWM 整流器的数学模型为：

令交流侧电压矢量在d,q 轴上的分量分别为upd=UdcSq,upq=UdcSd.在式(6)中，d,q 轴变量互相耦合，因而不能对其电流进行单独控制。通过id,iq的前馈解耦控制，对ud,uq进行前馈补偿，并且采用电流预测法对电流环进行控制，方程如下：
式中：id* 为电压环PI 的输出值;iq*=0.
将第k+1 次
采样周期时输入电流的采样值，用给定值id*(k+1)，iq*(k+1)来代替，计算出符合电流变化的输出电压矢量。在PWM 中运用空间矢量法合成输出电压矢量，使下一次采样时刻的实际电流以最佳特性跟随下一时刻的参考电流。

控制系统的电压外环采用PI 调节器，其输出得到三相参考电流幅值基准i*,i* 就是d,q 旋转坐标系下的电流给定值id*(k+1)，iq*(k+1)。只要在开关周期内实现式(7)，即可实现电流无差拍控制。