快速色彩平衡算法分析

in的值全部改成Vmin，把大于Vmax的值全部改成Vmax。执行过程中，首先需要优化一些极端值，优化的极端值数量由输入的优化率s决定；再根据s为整幅图像分别确定一个合适的最大值Vmax和最小值Vmin，颜色值在[Vmin，Vmax]范围外的像素即为极端像素，将极端像素的值改在[Vmin，Vmax]范围内，最后再根据Vmin、Vmax和s按比例来提高非极端像素的颜色值。

　　

1 新型色彩平衡算法

本文中算法的理论基础是在RGB模式中颜色值越高越接近白色，颜色值越低越接近黑色。如果图像是在黑暗中拍摄的，其像素最高的颜色值一定小于255，则通过扩大颜色值的范围，图像就会变亮。例如，闪电的主要颜色是R和G，那么通过色彩平衡就要增强B，这样会减少一些微黄色色调，图像会更亮一些，不但增加了画面的和谐性，而且使图像看起来更自然。

算法算法可以理解为有基本运算及规定的运算顺序所构成的完整的解题步骤。或者看成按照要求设计好的有限的确切的计算序列，并且这样的步骤和序列可以解决一类问题。

综上所述，本算法的目的是增加R、G、B三个颜色通道的颜色值，并使它们的范围保持在[0，255]。最简单的实现方式就是给每个通道ax+b的颜色值。其中，a、b是比例因子，需要通过计算得到，x是初始颜色值，ax+b必须在[0，255]的范围内。

在实际图像中经常会遇到颜色值为0或255的像素。实际需要优化的点或许很多，或许只有一个，不好确定确切的数目，所以必须用优化率来决定究竟要改变多少个点的值。假设一幅图像上有N个像素点，优化率为s，则需要优化N×s个点，并使0<N×s<255。优化率的选取不能太大，因为需要优化的点通常只占很少一部分。

　　

2 新型色彩平衡算法实现过程

本文介绍了排序和直方图两种改进的算法来实现色彩平衡的过程，下面阐述两种算法的实现和实用性。

　　

2.1 排序算法

算法流程如下：

（1）排序

排序是计算机内经常进行的一种操作，其目的是将一组"无序"的记录序列调整为"有序"的记录序列。分内部排序和外部排序。若整个排序过程不需要访问外存便能完成，则称此类排序问题为内部排序。反之，若参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，则称此类排序问题为外部排序。内部排序的过程是一个逐步扩大记录的有序序列长度的过程。

将N个像素存入矩阵，并将它们按颜色值大小从低到高进行排序（排序之前要先将矩阵备份，因为以后还要用到）。

（2）确定优化数量和最大最小值

输入优化率s，则优化数量为N×s，需要优化的点是排序后的矩阵的前N×s/2和后N×s/2。因此，Vmin、Vmax分别产生在N×s/2和N×（1-s/2）-1的点。

（3）优化像素

将颜色值小于Vmin的全部改为Vmin，将颜色值大于Vmax的全部改为Vmax。

（4）生成颜色值范围为[min，max]的新图像

假设新颜色值为f（x）=ax+b（x为旧颜色值），则有：

　　

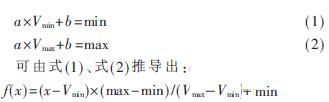
2.2 直方图算法

N个像素颜色值排序的时间复杂度是O（Nlog（N））。还有一种更高效的方法，即以直方图为基础的改编版本，最坏情况下其时间复杂度也仅为O（N）。

算法流程如下：

（1）建立一个关于像素颜色值的直方图

横向i表示颜色值，纵向表示≤i的像素数量q。

（2）确定优化数量和最大最小值

根据直方图表示的意义，柱的高度>N×s/2的最小颜色值i，即为Vmin；同理，柱的高度≤N×（1-s/2）的最大颜色值i，即为Vmax。如果s=0，那么i的最小值即为Vmin，i的最大值即为Vmax。

（3）优化像素

将颜色值小于Vmin的全部改为Vmin，将颜色值>Vmax的全部改为Vmax。

（4）生成颜色值范围为[min，max]的新图像

假设新颜色值为f（x）=ax+b（x为旧颜色值），则有：

 

 

对于16位像素值，直方图算法是非常好的算法，只需要大约256 KB的内存，得到Vmin和Vmax的速度非常快，其速度可与二分法媲美。

但对于32位像素值，直方图算法大约需要耗费18 MB内存。这种情况下，最好采用排序算法。

　　

3 实验结果

将本文提出的算法用于改善曝光不足或采光条件不好或特殊光线下（如日落）生成的图像的一种算法。该算法可以运用于大部分图像，即使原图是在正常光线下拍摄的也同样适用。

图1分别展现了原图分别经优化率为0%、1%、2%和3%的色彩平衡算法优化后的结果。由图可以看出，其图像的优化率不同，优化结果也不同。

与基于CCD或CMOS矩阵转换原RGB颜色为更加标准的感性颜色及白平衡算法等传统的色彩平衡算法不同，本文提出的新型快速色彩平衡算法，通过