基于特征模理论的系统天线设计方法

一、概述

不断提高通信系统的通信容量和质量，是无线通信的永恒主题。随着无线通信技术的迅速发展，人们对天线的设计提出了越来越多的要求。采用超宽带（UWB）技术和多输入多输出（MIMO）技术在提高数据传输率方面具有极大的潜力，MIMO技术能够提高通信系统的信噪比，提高信道容量及抑制信道衰落，对于移动设备来说，需要多单元集成在一起，以减小整个天线的尺寸，就要求MIMO多天线单元之间的互耦较低，以此来实现各路信号之间的低相关性。采用基于矩量法的特征模技术是一种最佳的选择。

特征模分析方法是近年来兴起的一种分析方法，它是应用较为广泛的矩量法结合解析本征模理论求解电磁问题的一类新方法。它为天线设计者提供了一种最佳的天线设计手段，有助于天线设计师了解天线的工作机理。利用分析得到的不同模式信息，掌握其谐振特性以及不同模式的辐射特性等，借助于不同模式特征电流的分布来选择最佳的馈电位置以激发出需要的模式，也有助于指导设计师对天线进行开槽来微调其谐振位置^[1]。本文采用FEKO V14版本^[2]的特征模分析工具仿真了几种常用天线形式的特征模参数。模式方法为任意复杂形状的电磁问题定义了一系列与解析法类似的本征模式，这些模式可描述电磁问题的本征特性，且模式之间具有正交特性，本征值的大小直接决定了该模式对电磁问题参量的贡献大小。它使得矩量法有了更为清晰的物理景象，天线设计者可以利用模式分析提供的信息，更深入地理解天线的工作原理，设计出性能最优的天线，甚至设计新的天线形式^[3]。

二、原理

特征模理论最初由Garbacz在1968年他的博士论文^[4]中提出，1971年由Harrington和Mautz通过对角化导体的广义阻抗矩阵，得到了与Garbacz定义的相同模式^[5]-[6]，在[5]中描述的被称为特征模式理论的公式相对于由Garbacz在[4]提出的更易于推导，并对任意形状的结构体进行了验证是非常有效的。后来Harrington等人对特征模理论进行了扩展，可以处理电解质、磁介质以及电/磁性混合体等^[7]。特征模理论自提出以来,在计算电磁学和天线设计等领域受到广泛关注。

特征模理论为任意形状的导体定义了一系列相互正交的特征模式,而这些相互正交的特征模式是导体的固有属性,本身具有收敛性和完备性，可以精确的表示电磁问题的解。特征模理论物理概念清晰,可以明确给出电磁结构体的工作机理,同时特征模式仅与电磁结构体的形状,尺寸和工作频率有关,与源点无关,因此便于指导工程设计。

特征模理论是建立在矩量法（MoM）基础之上的，其本征方程为：

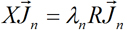 (2.1)

把导体上的电流用特征电流作为基函数展开为:

(2.2)

另外，经推导得到：

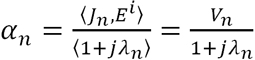(2.3)

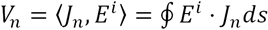(2.4)

在式2.3中展开系数α_n代表特征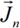电流在总电流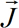中的重要性，称为模式加权系数Modal Weighting Coefficient (MWC)。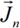为特征电流，λ_n为特征值，Eⁱ为入射场。在式2.4中，V_n为模式激励系数Modal Excitation coefficient (MEC)，当添加激励信号时，确定哪种模式容易被激发。

由于R,X均为Hermitian算子，同时也是实对称算子，算子R为正定算子,因此根据广义特征值及R,X 的性质，求出的特征值λ_n和特征电流J_n均为实数（即同相位）。可以证明，特征电流满足如下的正交性^[30]：

〈J_m , RJ_n〉=δ_mn (2.5-1)
〈J_m , XJ_n〉=λ_nδ_mn     (2.5-2)
〈J_m , ZJ_n〉=(1+jλ_n)δ_mn   (2.5-3)

这里，特征电流进行了归一化，即〈J_n , RJ_n〉=1。表示辐射功率为1。由于P_mn=〈J_m , ZJ_n〉，因此在辐射功率为1的情况下，储能只与λ_n有关，λ_n的正负号确定储能的类型：当λ_n越接近0，表示该模式在此频率下越接近谐振；λ_n＞0表示该模式在此频率下储存磁能；λ_n＜0表示该模式在此频率下储存电能。

由于λ_n的值变化范围很大，不便于观察，工程上也采用Modal Significance (MS)和特征角Characteristic Angle(CA)表示天线各个模式的谐振情况：

(2.6-1)

CA=180° -tan^-1 λ_n    (2.6-2)

由式（2.6-1）可知，MS的取值范围为（0，1 ]，当MS越接近1，表示该模式越接近谐振状态；反之，表明该模式远离谐振，难以被激励而有效辐射。由(2.6-2),当CA=180度时，表示该模式为谐振状态。

用MS参数可以定义模式的辐射带宽BW_n，即在频带范围内，辐射能量大于等于谐振点的辐射能量一半的频率范围。

(2.7-1)

(2.7-2) 

上式f_U 和f_L 即为MS值为0.707时的两个频点，f_res为当前模式的谐振频点，由（2.7-2）式就可以算出其带宽，同样，各个模式的工作带宽也可以在特征角（CA）随频率变化的曲线中读出，不难得到当各个模式的MS值=0.707时，对应的λ_n=1和λ_n=-1，CA=135度和CA=225度。