移相全桥变换器的建模与仿真
时间:01-08
来源:EDN
点击:
由于开关电源是一个线性与非线性相结合的综合系统,给系统的动态研究和设计带来很多不便。本文主要是用状态空间平均法来进行建立模型,它是由美国加里福尼亚理工学院的R.D.MiddlebrOOk于1976年提出的。这种方法不仅简化了计算过程,使各种不同结构变换器的解析模型具有了统一的形式,而且操作性更强,工作人员仍可以用波德图(Bode Plot)或者奈奎斯特(Nyquist)定理来对系统进行系统稳定的判定。
1 建模
由于移相全桥变换器可由Buck变换器变化而来,首先根据Buck变换器的原理,采用状态空间平均法,建立Buck变换器的小信号模型。为简单起见,本文简化变换器,使其工作在理想状态,即状态转换是瞬间完成的,在任何时候都只有两种状态存在--导通或关断。选择电感电流iL和电容电压Uc为状态参量,输出电压Uo和输入电流Is为输出参量,Ui为输入参量,D为晶体管占空比。如图l所示。


2)变换器工作在DCM状态下,由图3可知,在DTs≤t≤Ts时间段内,


二极管的导通占空比为D’=1一D,则基本的状态平均方程组为:

将上面各式代入到(10)式并减去式(11)得扰动方程为

由于变压器存在漏感Lr,使得移相全桥变换器的有效占空比为Deff,它总小于原边占空比D,则有效占空比的计算如下式:
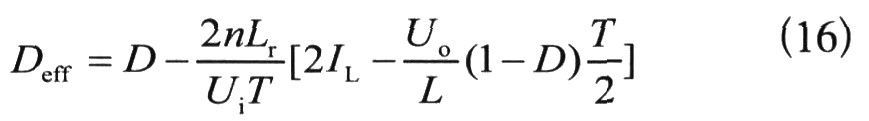
由(16)式可看出,IL、Ui、D的扰动都会使有效占空比Deff发生扰动,而这三种不同的扰动量di、du、dd的表达式分别为

从而得到移相全桥变换器的小信号等效电路模型如图4所示。
根据图4导出移相全桥变换器主电路的传递函数,

2 仿真
本文以一台实验样机的参数为指标,利用MATLAB对系统进行仿真,其参数如下:

3 结论
通过利用奈奎斯特判据先对系统开环进行仿真,如图5(a)所示,在右半平面内无极点,轨迹与实轴大约为0.678处,(0,j0)不在轨迹范围内,所以该系统开环是稳定的。通过加入单位阶跃效应构成闭环系统进行验证,如图5(b),可以看出系统是渐进稳定的。

1 建模
由于移相全桥变换器可由Buck变换器变化而来,首先根据Buck变换器的原理,采用状态空间平均法,建立Buck变换器的小信号模型。为简单起见,本文简化变换器,使其工作在理想状态,即状态转换是瞬间完成的,在任何时候都只有两种状态存在--导通或关断。选择电感电流iL和电容电压Uc为状态参量,输出电压Uo和输入电流Is为输出参量,Ui为输入参量,D为晶体管占空比。如图l所示。



2)变换器工作在DCM状态下,由图3可知,在DTs≤t≤Ts时间段内,


二极管的导通占空比为D’=1一D,则基本的状态平均方程组为:

将上面各式代入到(10)式并减去式(11)得扰动方程为

由于变压器存在漏感Lr,使得移相全桥变换器的有效占空比为Deff,它总小于原边占空比D,则有效占空比的计算如下式:
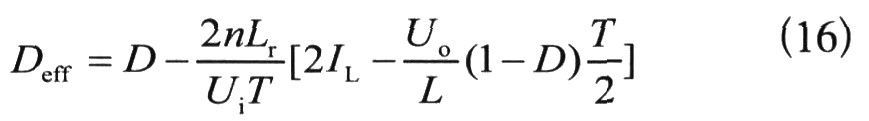
由(16)式可看出,IL、Ui、D的扰动都会使有效占空比Deff发生扰动,而这三种不同的扰动量di、du、dd的表达式分别为

从而得到移相全桥变换器的小信号等效电路模型如图4所示。

根据图4导出移相全桥变换器主电路的传递函数,

2 仿真
本文以一台实验样机的参数为指标,利用MATLAB对系统进行仿真,其参数如下:

3 结论
通过利用奈奎斯特判据先对系统开环进行仿真,如图5(a)所示,在右半平面内无极点,轨迹与实轴大约为0.678处,(0,j0)不在轨迹范围内,所以该系统开环是稳定的。通过加入单位阶跃效应构成闭环系统进行验证,如图5(b),可以看出系统是渐进稳定的。

- 基于AT89S52的智能快速充电器控制系统的设计与实现(01-06)
- 不连续模式反激变换器的基本原理和电路设计(01-05)
- 2kW新型推挽正激直流变换器的研制(01-05)
- 负输出罗氏变换器实用性剖析(01-09)
- 一种新型ZCS-PWM Buck变换器研究(02-20)
- 高效紧凑反激式变换器电信电源的设计(02-13)
