DC-DC开关变换器中混沌现象的研究综述
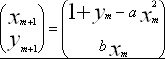 | (2) |
其中x=
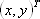
, a、b均是参数。因为必须把函数画在二维空间里,所以要看高维映射是较困难的,甚至n =2这种情况也不例外。同样,对于高维映射,满足
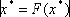 的矢量
的矢量 即为固定点。如当 a=1.4、b=0.3时,方程(2)有两个固定点,但都不具有吸引性,因而会导致混沌。
即为固定点。如当 a=1.4、b=0.3时,方程(2)有两个固定点,但都不具有吸引性,因而会导致混沌。3.3 数值仿真法
数字仿真是指利用各种各样的算法以求得变换器某些特性数字解的方法。它分为直接数字仿真法和间接数字仿真法两种。数字仿真的优点是准确度和精确度都高,可以得到响应的完整波形;适用范围广,可进行小信号分析和大信号分析。
由于混沌动力学系统的复杂性,很多混沌动力学系统不能用已知函数表示其通解,使得解析法很多时候无能为力,而且用解析法建模时,常常需要作出某些近似,以简化分析。众所周知,开关调压系统存在着功率级电路的开关非线性和控制电路中脉冲调制器的饱和非线性,因此不能用精确方法设计电路,也难以用解析法对混沌类现象进行有效的预测,同时这类系统受到的扰动常常是大幅度的,这时系统在大信号扰动下工作,对于大信号分析,一般很难用解析法求解,更需要借助于数字仿真,从而这就使通过数值计算来描述混沌行为的演化过程对开关变换器的混沌进行数值模拟显得十分重要[11]。
下面以PWM型BUCK变换器为例,用PSPICE对其进行仿真。如图,假定电路中的器件均是理想的,电路中参考电压Vref输入至反相器的反相端,R上的电压V(t)输入至误差放大器OA1的正向输入端,OA2的正向端为一个时钟信号--锯齿波电压,放大器产生一个控制信号,作用于PWM,与时钟信号比较。每周期初始,PWM输出脉冲,当反馈电路的输出端(即控制电压)高于锯齿波电压时,输出为高电平,压控开关导通;当锯齿波电压上升到控制电压时,输出脉冲截止。直到下一周期开始,再次输出脉冲。因此控制电压的波形决定了输出脉冲的宽度,进而决定了开关管的导通时间。这样产生一系列的脉冲信号来控制主电路的压控开关的。电路中的参数值如下: 输入电压Vs=10v ,电容C=100uf,电感L=100uh,负载电阻R=22, 参考电压Vref=5v,锯齿波电压Vpulse(0v,10v,0s,199.99u,0.005u,0.005u,200u),放大器的放大倍数e=15,稳态时,变换器的输出含周期性的纹波,然而某些情况下,电路会发生多脉冲现象,开关通断多次,从而增加了开关损耗,变换器的效率降低。我们用PSPICE仿真后可得,如下图: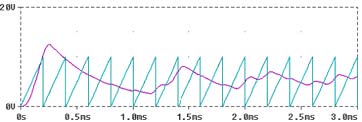
4 稳定性及稳定条件
一般的,稳定的DC-DC变换器表现为周期性的稳态。一旦初始暂态值衰减,状态变量就以周期重复。控制相应的离散系统的映射有一个吸引性固定点:在周期性的稳态,每一个周期都与下一个相同,所以在每个周期采样得到的情况都一样。若变换器是局部渐近稳定,相应的一个小的扰动它会使周期稳定下来,这个离散系统相应的序列会收敛于这个固定点,因此,这个点是吸引子。相反,若变换器初态是不稳定的,这个序列会偏离固定点。因此,可以得出结论:映射的固定点的稳定性决定连续系统的局部稳定性。一个吸引性的固定点对应着连续系统的周期性的稳态。
一阶系统稳定的条件是映射在固定点处的梯度在-1和1之间。 即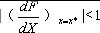
固定点的稳定性也可以推广到高阶。不同的是,一阶的稳定性由梯度决定,而高阶由特征增益率决定,固定点的特征增益率是映射在固定点处的雅可比阵的n个特征值。其中雅可比阵是对各个元素求X偏导后所得矩阵。高阶系统稳定的条件是若特征增益率都落在复平面上的单位圆之内,则固定点稳定。
5 混沌的研究状况
因为分叉、混沌等不稳定现象与系统的非线性密切相关,所以在分析研究时必须跳出线性电路的范畴[12].目前最常用的方法是一维映射法。一般的,开关变换器的离散表达式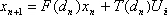 可写作
可写作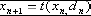 ,其中
,其中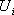 为输入,
为输入,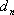 是第N个周期的占空比, F、T分别是系数矩阵的指数函数。对于闭环工作的开关变换器,一般有
是第N个周期的占空比, F、T分别是系数矩阵的指数函数。对于闭环工作的开关变换器,一般有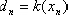 ,
,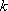 是非线性函数,因而
是非线性函数,因而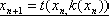
,这就是一维映射法的原理[13].现在已有比较成熟的理论。文献[10,5,14]使用该法分析了电流反馈的变换器的分叉混沌现象。最近,Tse的一系列工作如[15]都是推导出该一维映射的解析表达式,通过研究这一映射来得到变换器的动力学性质,揭示了变换器从倍周期、分叉走向混沌的具体过程。
另外,从国内外
- 新型灌封式6A至12A DC-DC μModule稳压器系列(11-19)
- 数码相机电源电路设计及DC/DC变换器选择(01-22)
- 产生双极性输出的无变压器 DC/DC 变换器(01-23)
- 改进型全桥移相ZVS-PWMDC/DC变换器(01-23)
- 为DC/DC转换器选择正确的电感器与电容器(01-02)
- 开关DC-DC转换器的EMI方案(04-29)
