CVCF逆变器波形控制技术研究

控制理论中的内模原理[3],即如果希望控制系统对某一参考指令实现无静差跟踪，那么产生该参考指令的模型必须包含在稳定的闭环控制系统内部。图一是本系统采用的重复控制框图，以下对其各部分进行分析说明。

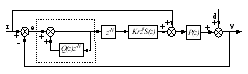
图1　离散域重复控制器框图

P(z)是逆变器的输入与输出的离散传函，是系统中的控制对象。逆变器的开关频率比LC滤波器的自然频率高得多，其动态特性主要由LC滤波器决定，通过建立系统状态方程获得P(z)。本系统中，L=0.88mH，C=60µF, 电感的等效串联电阻为0.4Ω，开关频率和采样频率都是10KHz，推导出其离散传函为：

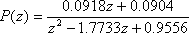
作出其伯德图如图2所示，可以看到逆变器存在一个谐振峰，阻尼比很小。

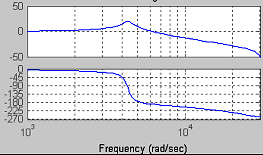
图2　逆变器P(z)的伯德图

图1中虚线框内为重复控制器的内模，N为一个周期内采样的次数。该内模实际上是一个周期延迟正反馈环节，只要输入信号是以基波周期重复出现，其输出就是对输入信号的逐周期累加。当Q(z)取值为1，可视为以周期为步长的积分环节，可以达到无静差，但是给系统带来N个位于单位圆周的极点，使开环系统呈现临界振荡状态，本系统中Q(z)取为0.95，以改善系统稳定性。

图1中重复控制器里包含有一个补偿器

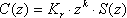
其中滤波器S(z)由以下两部分构成

 

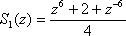
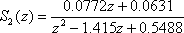
陷波滤波器S1(z)主要用于对消逆变器的谐振峰值，二阶滤波器S2(z)主要提供高频衰减。超前环节zk 补偿滤波器S(z)和控制对象P(z)总的相位滞后，Kr 是重复控制增益。补偿器C(z) 要达到的目的是使校正后的对象中低频增益接近于1，而高频增益则尽快地降至-26dB以下，同时系统在整个中低频段前向通道的总相移尽量小。取Kr =0.9，zk =z5 ，作出C(z)P(z)的伯德图，如图3所示，可以看到设计符合要求。

 

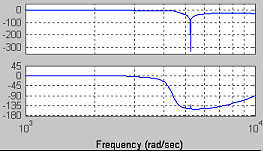
图3　C(z)P(z)的伯德图

前向通道上串接的周期延迟环节z-N使控制动作延迟一个周期进行，即本周期检测到的误差信息在下一周期才开始影响控制量。引入周期延迟环节的主要原因是系统中含有超前环节zk，如果此系统要能够物理实现，必须有一延迟环节。

3　极点配置

重复控制有效的改善逆变器稳态性能，但动态响应欠佳。实际上，逆变器的自然动态特性之所以不好，最主要的原因是逆变器自身的阻尼太弱。对此，最直接有效的解决办法就是引入状态反馈，进行极点配置，增加控制对象的阻尼。

图4是为单相逆变器的等效电路，逆变器空载时阻尼最小。因此，在实施极点配置时，假定逆变器处于空载(最恶劣的情况)，配置极点时应注意逆变器带载以后阻尼比会变大。

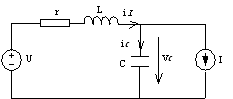
图4　单相PWM逆变器模型

取电容电压vC和电容电流iC作为状态变量，PWM逆变器的空载模型为：

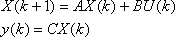
引入状态反馈

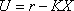
，其中r 是闭环系统参考指令，K是反馈增益阵，则闭环系统的状态方程变为：

将闭环极点配置在z域的0.74±0.3i点，此时系统自振荡频率ωn为4454rad/s(大致与LC滤波器截止频率相同);阻尼比ξ为0.5。图5(a)是系统的突加负载仿真波形,观察发现输出电压在突加瞬间跌落后不能完全回到原来的轨迹，而是有一个固有的静态误差。对反馈系统分析发现，电容电压vC 反馈相当于一个比例环节P，电容电流iC 反馈相当于一个微分环节D，都不能消除静态误差。因此，我们在控制系统中引入积分环节，把输出y的积分量和状态变量一起作为反馈量，假设这个新变量为xI，即

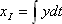
，原来的二阶系统变为了三阶系统

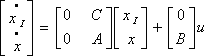
新增一个配置极点在z域的0.1，此时系统的突加负载仿真波形如图5(b)所示，我们可以看见原有的静态误差已经被消除。

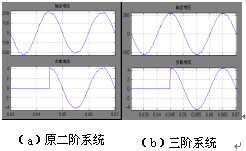
图5　突加负载仿真对比

4　复合控制

综合以上两种控制方案构成整个控制系统，其中，状态反馈极点配置控制居于控制系统内层，其目的是通过重新配置极点来改善系统的动态响应特性。重复控制居于控制系统外层，其主要目的是减小非线性负载等因素造成的谐波失真。只要极点配置和重复控制单独作用时系统稳定，那么复合系统就是稳定的。

5实验结果

图6是极点配置系统带整流型非线性负载的波形，THD值为6.89%。图7是加上外层的重复控制后的非线性负载工作波形，负载电流峰值15A, THD值降为1.42%，分析电压频谱发现13次以下的谐波幅值有明显的衰减，这验证了重复控制的谐波抑制能力主要体现在中低频段。图8是复合系统突加5A的阻性负载电压波形，系统很快结束过渡过程，同时也基本消除了静态误差。

6　结论

本文分析了重复控制和极点配置两种控制方式在数字化CVCF逆变器中的应用，提出了一种基于重复控制和极点配置的复合控制策略。实验结果证明该策略使系统得到了比较理想的稳态特性和动态特性，而且易于实现，有一定的实用价值