基于ADSP2189常用图像处理方法

近几年来，Analog Devices公司的ADSP系列数字信号处理器以其优异的性能和简单易学的语言逐渐受到人们的青睐，其中的ADSP218X定点系列更是得到广泛的应用。ADSP2189片内有192KB的RAM，因此更多地应用于图像领域。本文就图像处理压缩过程中常用到的算法及其在ADSP2189上的实现进行了分析，如何充分利用ADSP系列数字信号处理器特殊的硬件结构和功能强大的指令集实现各种算法是本文讨论的重点。然而作为通用定点处理器，处理过程中如何避免可能出现的问题以及如何解决问题也是本文所要讨论的。

1 ADSP2189及EZ-KIT简介

ADSP2189是指令执行速度最高可达75MIPS的16位定点数字信号处理器，主要具有以下特点：单周期指令执行，片内的程序控制器不会附加循环和条件指令的执行周期；三总线的体系结构允许在单指令周期中进行双操作数传递；片内192KB的存储器可被配置成32K×24bit的程序区(PM Program Memory)和48K×16bit的数据区(DM: Data Memory)，而ＰＭ中还可同时存放数据。除了具有优异的计算能力外，ADSP2189还具有强大的系统接口：8位的BDMA端口寻址可达4MB，用来提供片内外存储器的高速存取；16位的IDMA(Internal Direct Memory Access)端口可实现主系统对片内存储器的高速存取；2048个I/O地址，支持并行的外设；两个双缓冲串口，带自动压扩。

ADSP-2189M EZ-KIT Lite是一块可用来演示验证DSP基本算法的仿真板，也是本文所有算法的测试平台。它主要由以下器件组成：

·ADSP-2189M 75 MIPS DSP
·AD73322立体声编译码器
·RS-232接口
·FLASH存储器

EZ-KIT Lite的FLASH存储器中带有监控程序，这段程序可完成仿真板与PC机间的串行通信，并允许用户下载、执行和调试ADSP2189程序。EZ-KIT Lite可与EZ-ICE仿真器相连，通过EZ-ICE仿真器，用户可以单步执行程序、观察和改变寄存器和内存值以及完成其它调试工作[1]。

2 模板运算

在图像处理时，模板运算有着广泛的应用。例如，在边沿检测时，通过将像素矩阵与边沿检测矩阵即模板相卷积来实现检测功能；在图像平滑时，通过模板运算来滤除噪声。模板运算的数学涵义就是卷积(或互相关)运算[2]，它是一项非常耗时的运算。以模板1/16[1 2 1 2 4 2 1 2 1]为例，每个像素完成一次模板操作要用9个乘法、8个加法和1个除法。对于一幅N×N的图像，就是9N2个乘法，8N2个加法和N2个除法，算法复杂度为0(N2)。一幅较大的图像计算量是很大的，所以很多专用的图像处理系统，用硬件来完成模板运算，这样可以大大提高速度。在ADSP2189上快速实现模板运算需要充分利用ADSP2189的结构特点和功能强大的指令集。由于ADSP的哈佛结构允许同时访问程序和数据存储器，而ADSP的多功能指令(Multifunction Instructions)在执行算术操作的同时还可以并行进行数据传输，因此在单周期内可以完成取指、译码、读数、执行和调整寄存器。例如，MR=MR+MX0*MY0(SS)、MX0=DM(I0，M0)、MY0=PM(I4，M4)，MX0和MY0分别从数据和程序存储区以间接寻址方式取得操作数相乘，乘积与结果寄存器中数值相加后放回结果寄存器，数值计算的同时地址指针寄存器I0、I4中的地址自动与调整寄存器中M值进行相加更新。虽然ADSP2189支持除法指令，但为了提高速度，可在程序中将除法改为乘以除数的倒数。另外，在程序中将２维模板运算转换成1维模板运算，可极大地降低运算量。需要注意的是，由于ADSP2189中CNTR寄存器为14bit，所以在单循环处理中输入像素个数必须小于16383。模板运算程序的流程如图1所示。

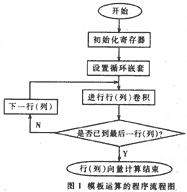
以3×3模板为例，通过在Visual DSP环境下设置PROFILE选项，可以得到以下结论：对于一个100×100的数组，完成模板运算共需要96445个指令周期；对于一个640×480的数组，共需要3052205个指令周期，远远低于直接计算。

3 DCT变换

许多图像压缩算法采用DCT(Discrete Cosine Transform，即离散余弦变换)来消除像素间冗余，例如JPEG 、H.261以及MPEG。采用DCT是因为它具有以下优点：DCT不同于DFT(Discrete Fourier Transform，即离散傅立叶变换)，它属于实域运算；DCT变换矩阵的基向量很接近于托波列兹矩阵的特征向量，所得变换系数具有弱相关性，可以单独处理各系数而不损失压缩效率。

一维DCT表达式如下：

二维DCT表达式如下：

式中

由上面的表达式可以看出DCT属于可分离变换，所以二维DCT通常不采用直接计算的方式，而是对原始图像数据的行和列分别做一维DCT，即将图像数据的各行做一维DCT，然后将结果矩阵各列再做一次一维DCT。以8×8的图像块为例，进行行列一维DCT需要1024次