基于VxWorks平台的快速交流信号采样及计算

上世纪90年代，以微处理器为核心的数字式保护已成为继电保护的主流产品，电力系统继电保护技术进入了微机保护时代。随着电力系统对继电保护的要求不断提高，微机保护系统需要具有强实时性、高可靠性和扩展性[1]。

系统的实时性由硬件系统和嵌入式软件系统共同决定。

在实时性要求较高且任务较多的应用中，适合引入嵌入式实时操作系统RTOS(Real-Time Operating System)。RTOS高效的多优先级任务管理、强大的可移植性和扩展性以及微秒级的中断管理等特性，更加有利于控制效率的提高。VxWorks是硬实时特性最优越的RTOS，且具有高可靠性和可扩展性，能够为继电保护装置提供更好的性能保障。

1 继电保护装置软件系统

1.1 工作原理及流程

目前典型的继电保护装置应用软件系统均采用模块化设计思想，根据继电保护功能的要求分成8个部分：操作系统、交流采样、数据处理、保护控制、数据通信、人机交互及信息记录。各模块根据各自特点完成相应任务，使系统软件结构清晰，便于调试、连接、修改和移植。

1.2 系统软件框架设计

根据所要实现的功能和软件模块化设计的要求，设计了基于VxWorks的系统软件，包括硬件驱动程序模块、板级支持包（BSP）模块、VxWorks RTOS模块、中断处理模块、保护控制模块、人机交互模块、通信任务模块、信息记录模块等。系统软件框图如图1所示。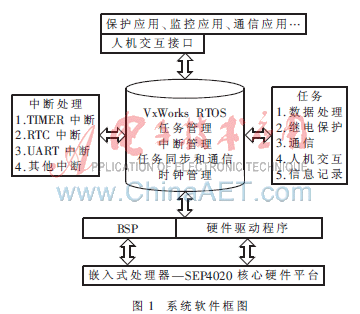



2 交流采样功能设计与实现

2.1 中断服务

由于A/D采样对实时性要求极高，因此采用中断服务子程序的方式实现。本设计利用Timer的定时中断控制A/D采样的频率，利用VxWorks提供的接口函数intConnet()将A/D的采样函数挂靠到定时中断Timer1的中断向量上。

继电保护的交流采样可以分为数据采样和采样数据处理两部分。数据采样在采样定时周期控制下，将A/D转换好的数据通过SPI总线送到CPU采样数据存储区。采样数据处理则是CPU对已采样数据进行傅氏滤波、提取交流信号的各电气量参数。该部分软件的计算量需求是所有程序中最多的，因此是优化的关键部分。

2.2 数据采样

数据采样首先要考虑AD采样精度和采样率。采用ADI公司的12 bit ADC AD7940，针对所要采样波形的最高频率是工频5次谐波的要求，选择了1 kHz采样率，即每周波采样20个点。
在采样定时周期中断到来时， ADC开始启动13路模数转换。一路采样完毕之后，通过SPI总线传送到定义的采样数据存储区；当13路数据传送完毕，就可以进行采样数据的傅氏滤波处理，计算出三相交流电的电流、电压的幅值和相位。

2.3 数据处理

2.3.1 离散傅氏算法

交流采样数据的处理是系统计算工作的核心，它的实时性和精度决定了保护任务的实时性和系统响应的准确性，从而影响整个系统的性能实现。因此，交流采样数据处理算法的选择十分重要。虽然快速傅氏算法(FFT)理论上要比离散傅氏算法(DFT)具有更高的速度[4]，但在继电保护应用中，考虑到采样点数、计算量以及系统的实时性需求，采用了DFT作为处理算法。

根据傅氏级数原理，各次谐波分量的实部和虚部的时域表达式为：

当傅氏分析方法应用于计算机处理时，即为DFT形式。设信号x(t)每周期的采样点数为N，则采样间隔将是Ts=T/N，则式(1)、式(2)离散化后得到DFT的公式可表达为：

从式（3）和式（4）得出，使用DFT算法计算信号的一个谐波分量，共需 2N次乘法和(2N-1)次加法，这样每次抽样所需计算的数据量非常大，而且随着N的增长，计算量将显著增加。

根据一般电力系统继电保护的应用，本文对13个通道的电流和电压信号进行采样，在每周波采样20个点的情况下，为了得到每个通道的幅值和相位，总共需要计算520次正余弦、520次乘法、507次加法、13次开平方和13次反正切，因此需要采用优化措施以减小计算量。

2.3.2 实时性优化

(1)快速查表

为了避免在傅氏运算中计算sin(2πk/N)、cos(2πk/N)(k=0，1，2，…，N)等三角函数的值，在系统初始化时应将这些值事先计算出来并保存到一个表中，运算过程中以查找表的形式直接获取正余弦函数计算的值。

(2)定点乘法

AD7490输入模拟电压范围是0 V～5 V，对应的输出数字范围是0x00～0xFFF。由于SEP4020处理器不支持浮点运算，所以对小数的运算将非常耗时。为了避免进行小数运算，采用了小数定点运算方法，用整型替代实型运算。这里定点的定标设为15，整型数0x8000就对应实型数1.0。

为了保持定点运算，避免sin(2πk/N)、cos(2πk/N)带来的小数运算，这里对sin(2πk/N)、cos(2πk/N)计算出来的值进行定点化处理，并将其乘以2的15次方取整后得到16 bit的有符号整数。这样傅氏算法的循环浮点乘操作就转变成整数乘法，既保留了傅氏算法的高精度特性，又极大地提高了傅氏算法的计算速度。

(3)快速开方

在利用傅氏计算得到的实部和虚部求幅值时，需要进行开平方运算。而在RISC内核的嵌入式处理器中，如果不对开平方运算做特殊处理，则CPU的运算时间较长，将影响整个系统的实时性，因此考虑采取快速算法来提高开平方运算的速度。

本文的开平方运算对象是无符号的整型数，可以采用一种只利用移位、加法实现整数开平方算法的方法。由于RISC内核中有内置的桶型移位器，因此该算法可以用汇编程序实现[6]。
整数快速开方算法函数的代码如下：
unsigned long isqrt(unsigned long x)
{
unsigned long temp,Q=0,b=0x8000,bShft=15；
__asm
{
mov b,#0x8000
mov bShft,#15
mov Q,#0
loop:
add temp,b,Q,lsl#1
subs temp,x,temp,lsl bShft addge Q,Q,b
movgex,temp
sub bShft,bShft,#1
movs b,b,lsr#1
bne loop
}
return Q；
}