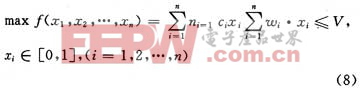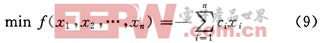基于具有量子行为的粒子群优化算法惯性权重研究及应用

表1的数值是对每个函数在粒子数为20个的条件下，测试50次，然后取平均得到的结果。从表中可以看出，对于函数F1(x)，比较结果可以明显得知：在随粒子群维数增加的情况下，ω1-QDPSO是比QDPSO得到更好的解，其他几种改进方案的解都比较差；函数F2(x)在随粒子群维数增加的情况下，4种改进方案和QDPSO都能得出比较好的解。

通过实验，可以看出：对于单峰函数F1(x)，ω的递减不能太小，从方案ω1-QDPSO和ω2-QDPSO的结果就可以比较出来，而方案ω3-QDPSO和ω4-QDPSO的结果不好，可能是因为它们搜索的区域太小，从而陷入局部最优解。

对于多峰函数F2(x)，ω的变化对测试函数的解的精确度没有太大影响，说明了改进方案在此方面没有明显提高。接下来，我们还对算法的收敛速度进行了比较。结果如表2所示。

表2是对函数测试50次后取得平均值的结果。可见对于函数F1(x)，ω1-QDPSO和QDPSO都在10维的情况下收敛，而20维时只有ω1-QDPSO收敛，其他函数都没有收敛，导致这种结果的原因有2种：

(1)各种方案随ω的变化，削弱或失去了调节能力，在达到最大迭代次数时也未收敛；

(2)即使在算法已搜索到最优解附近时，由于局部搜索能力太差，跳过了最优解。对于函数F2(x)，ω3-QDPSO，ω4-QDPSO，QDPSO收敛速度都比较快，ω1=QDPSO和ω2-QDPSO的收敛速度就相对较慢一些。这是由于对多峰函数测试时，各种方案的初始化范围附近可能存在最优解，所以减少了迭代次数，加快了算法速度。

通过对4种方案的研究，这里选取方案1应用于0-1背包问题，并得到理想的结果。

2 对改进算法应用到0-1背包问题

2.1 0-1背包问题的数学描述

0-1背包问题是一种典型的组合优化问题。0-1背包问题的描述如下：假设有n个物品，其大小和价值分别为wi和ci(其中wi>0，ci>0，i=1，2，…，n)，背包的容量假设为V(V>0)。要求在背包的容量限制内，使所装物品的总价值最大。该问题的数学模型可表示为：

其中，当将物品i装入背包时xi=1；否则xi=0。

2.2 0-1背包问题的改进粒子群算法

改进粒子群算法应用到0-1背包问题的思想：粒子群中粒子的个数与每个粒子的维数相等。先定义二进制数x，x只能取0和1。再把粒子的种群数看作背包的个数n，对于每个粒子xi(其中i=1，2，…，n表示粒子个数)有n个维数，即1个粒子有n个位置。然后初始化每个粒子的速度vij，(其中j=1，2，…，n表示每个粒子位置的维数)，每个粒子的每一维都对应一个初始化了的速度。对公式(8)进行变化：

解决背包问题的步骤：

(1)初始化粒子的速度和位置；

(2)将初始化的位置向量代人式(9)，在所得每个粒子的解中找到最优解pbest，并令pbest=gbest；

(3)通过式(6)更新粒子的速度，对所得最优解进行修正，然后再次代入函数方程中继续寻找新的最优解；

(4)若达到终止条件，则结束迭代，输出到存储向量，即为所求结果；否则，k=k+1，转步骤(3)。

2.3 实验仿真

为了验证ω1-QDPSO求解0／1背包问题的可行性及有效性，这里进行了2组实验，每组实验用ω1-QDPSO算法进行测试，每组算法运行50次。

实验一：取参数popsize=10，dimsize=10，c1=c2=2.05，genmax=1 000，g=0.968 5；N=10，V=269，W={95，4，60，32，23，72，80，62，65，46}，C={55，10，47，5，4，50，8，61，85，87)，得到实验结果是max f=295，收敛平均迭代次数11。

实验二：取参数popsize=20，dimsize=20，c1=c2=2.05，genmax=1 000，g=0.968 5；N=20，V=878，W={92，4，43，83，84，68，92，82，6，44，32，18，56，83，25，96，70，48，14，58}，C={44，46，90，72，91，40，75，35，8，54，78，40，77，15，61，17，75，29，75，63}，得到实验结果是max f=1024，收敛平均迭代次数23。

ω1-QDPSO算法求解0-1背包问题，与文献[9]中提出的用带有死亡罚函数的粒子群优化算法求解0-1背包问题相比，其运行速度明显提高。

3 结 语

本文通过采用4种方案对具有量子行为的粒子群优化算法的惯性权重研究分析表明，QDPSO改进算法中惯性权重的改变对性能的影响与经典PSO算法相比既具继承性又具发展性，在算法精度上ω1-QDPSO的结果比较优，而在计算速度上ω3-QDPSO和ω4-QDPSO的结果更优。选择其中算法性能相对较好的ω1-QDPSO算法应用于0-1背包问题，可以看出改进算法性能的改善在应用中得到更好的体现