OFDM的频率同步算法
文中提出的频率同步方法是在取得时间同步后,将接收的每PN序列长度的数据与本地PN序列作相关,共得L个值,分别为c1,c2,…,cL,

其频率估计范围为|ε|N/(2PK)。该同步方法在AWGN信道下较好,但在Rayleigh多径信道下性能较差。若应用于BEYOND 3G系统,就不能满足系统要求。故提出了另一种频率同步方法,此方法是在时间同步后,在接收数据每相邻的两个PN序列作共轭相乘后相加,利用相加结果的相位进行频率偏移估计。根据下式求频率偏移(此频率偏移估计方法称为方法二)

由式(7)得知,当被估计的频率偏移值越小,频率偏移估计值越精确;参数P越大,估计出的频率偏移越精确。
频率同步算法的性能
在BEYOND 3G系统中,假设载频fc=2 GHz,N=4 096,Ng=1 024,K=127,P=1,一个OFDM符号共5 120个抽样点,每一个子载波为5 kHz。当振荡器不稳定系数为ko=10−6,车速v=500 km/h,可计算出由振荡器不稳定和Doppler频移造成的频率偏移为fcko+fcv/c=20 kHz+1 kHz=21 kHz,相当于4.2个子载波,即频率偏移最大值不超过4.2个子载波,|ε|4.2。P=1时,方法1、方法2估计的频率偏移范围理论值不超过±16.12(N/(2K)=16.2)个子载波。若增大P,频率估计范围会降低,但估计精度将提高。
在AWGN的信道下,方法2频率同步的估计均方差比方法1频率同步的估计均方差要大,当不小于15 dB时,两者的值接近。在AWGN信道下,仿真10 000个符号,不同信噪比下频率偏移估计的均方差(MSE)的仿真结果见图2和图3。分别是不同P下的频率偏移估计的MSE。可以发现,当P取得较大时,相同信噪比下,其频率偏移估计精度得到了较大的提高。
Rayleigh信道下两种频率同步算法的性能比较如图4,图5所示,图中N=4 096,K=127,P=1,10 000个符号仿真,分别仿真了两种移动速度下的频率偏移估计的MSE。方法2在Rayleigh信道下比方法1要差得多的原因:方法1由于PN序列的良好相关特性,接收信号与本地PN序列作相关计算时,接收信号中只有最强径被利用,其他径信号由于与本地PN序列不同步,不能被利用,故方法1频率估计性能要差;方法2是接收信号内部作相关,可以利用大多数径的信号,故频率估计性能较好。
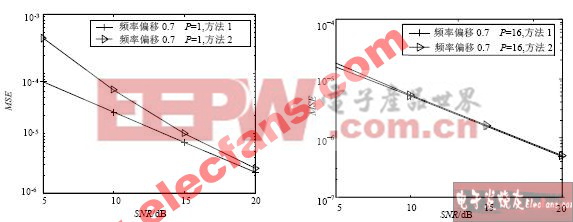
图2 AWGN信道下两种方法的频率估计性能比较 图3 AWGN信道两种频率同步方法性能比较
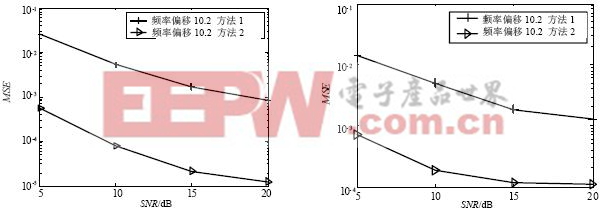
图4 车速为3 km/h时Rayleigh信道下两种方法的 图5 车速为60 km/h时Rayleigh信道下两种方法的
频率估计性能比较 频率估计性能比较
本文讨论了利用重复的PN序列作训练序列的OFDM频率同步,这种频率同步包括了频率粗同步和频率精同步。并利用多径信道中的多径信号对原方法进行了改进。该方法可用于Rayleigh信道下中等车速的(60 km/h)大范围频率偏移(频率偏移达十几个子载波)估计,其估计精度可以满足OFDM系统在Rayleigh信道下对频率同步的要求。
- 用FPGA实现FFT算法(06-21)
- FIR数字滤波器分布式算法的原理及FPGA实现(08-07)
- 基于算法的DSP硬件结构分析(04-02)
- 基于DSP的音频会议信号合成算法研究(05-10)
- 基于DSP的Max-Log-MAP算法实现与优化(05-27)
- 一种长序列小波变换快速算法的DSP实现(08-11)
