整周模糊度的快速求解算法
时间:06-06
来源:互联网
点击:
1.1 备选整周模糊度解集的确定
利用GPS双差载波相位测量时,其数学模型为: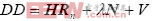

P0/0、X0/0初值的选取取决于对基线向量和初始模糊度范围的了解,基线分量及其变化速度分量初值可取为零,方差初值根据载体的动态情况选择,整周模糊度分量初值可取为伪距双差观测值,方差初值根据伪距的测量精度选择。
如果系统动态模型建立得比较准确(如静态时或载体运动规律已知时),则当卡尔曼滤波器稳定后,整周模糊度估计值一般具有较高的精度,可以直接取与其最接近的整数作为整周模糊度,但一般需要较长的时间才能得到正确的模糊度,对于实时性要求较高的场合不适用。实际应用时一般是当Kalman滤波达到一定



图1 整数高斯变换前的置信椭圆 图2 整数高斯变换后的置信椭圆
为进一步减少备选整周模糊度组合,将所有的使用卫星分为两组:选4颗卫星作为主组,用来确定模糊度的搜索空间,其余卫星作为从组,用于模糊度的检验。
对选为主组的4颗卫星,取其双差模糊度的浮点估计值及其方差阵进行高斯变换,得变换后的模糊度估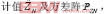 ,将对主组双差模糊度按式(16)确定的置信空间中的所有组合作为备选整周模糊度解集。
,将对主组双差模糊度按式(16)确定的置信空间中的所有组合作为备选整周模糊度解集。
- 用FPGA实现FFT算法(06-21)
- FIR数字滤波器分布式算法的原理及FPGA实现(08-07)
- 基于算法的DSP硬件结构分析(04-02)
- 基于DSP的音频会议信号合成算法研究(05-10)
- 基于DSP的Max-Log-MAP算法实现与优化(05-27)
- 一种长序列小波变换快速算法的DSP实现(08-11)
