一种基于密度的聚类的算法

j）=j;

j++;

end

end

sort（sum（：））；

S’（1,:）=count（，：）；

S’（1,n+1）=meanradius;

S’（1,n+2）=meandistance2;

If meandistance1meandistance2

If meanradiusnewmeanradius

Add xj to S’（1）；

S’（1,n+1）=new meanradius;

Else

Next class;

End

If no class

Create a new class S’（2）；

End

…

Until no data come

It’s over

Output S’

}

3 算法性能及分析

对M-DBSCAN算法的性能作了测试，并与DBSCAN作了比较。所有的测试都在1台PC机上进行，配置P4，2.0 GHz CPU，512 MB内存，80 GB硬盘，算法用Matlab7.3实现。

首先用构造的模拟数据对聚类结果进行验证。图2为DBSCAN算法在阈值半径为20时得到的结果，明显地将不同的三类作为一类输出，形成了错误的类划分；而在取同样的初始阈值半径时，图3可以看出M-DBSCAN算法得到更好的聚类结果。

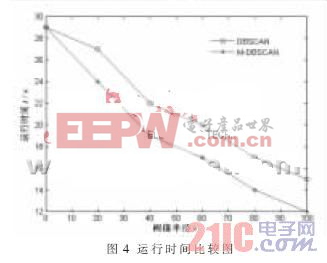
从图4中可以看到两种算法在SEQUOIA 2000数据库上对不同数据量样本的执行时间的比较。算法M-DBSCAN比算法DBSCAN快得多，且随着数据量的不断增大，这种速度上的差别越来越大。表1为两种算法的错误率比较图，错误率为，N1为算法所得聚类数目，N2为实际聚类数目。表1中可看出，改进的M-DBSCAN算法错误概率普遍要小于DBSCAN的，表明改进后的算法减小了错误率，对处理大样本集有较好的性能。

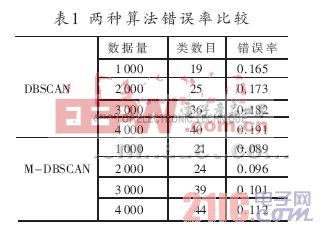
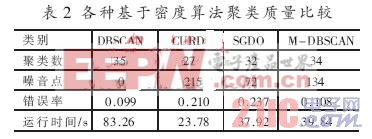
表2中的测试数据集来自Dr.JSrg Sander提供的仿照DBSCAN 中DataBase2生成的数据集DB2[8]。由表中可以看出，当数据规模为50 000时，虽然SGDO[7]处理噪音点的能力比M-DBSCAN强，但是从错误率和运行时间上M-DBSCAN比前两者都有较大的改善。CURD虽然有较短的运行时间，但是存在大量的噪音点。

本文讨论了一种将DBSCAN聚类算法进行改进的M-DBSCAN聚类算法，它克服了DBSCAN聚类算法不能处理大数据集的问题，并实现可以对阈值进行实时更改。试验结果显示，M-DBSCAN算法的准确性比DBSCAN算法要好，处理大数据集的速度更快。但是对于聚类数目的确定仍然是判断是否超过某阈值才可算作某一类的标准，聚类数目与阈值的选择有很大关系。因此如何自动确定聚类数目将是下一步工作的方向。