基于μC/OSⅡ的实时任务模型设计

本文通过研究实时操作系统内核及应用技术，分析实时操作系统性能指标；基于实时操作系统μC/OS Ⅱ内核接口和任务运行原理，提取实时任务的构成要素，构建实时任务模型。运用任务模型进行实时任务、实时应用程序的设计和实现。根据任务模型设计实现一个范例程序的基本功能和性能需求；将模型设计思想应用于实时软件开发，任务模型为实时程序研发和相关教学活动提供了一个简便的解决方案。

1 实时软件技术及实时软件构成

实时软件开发环境一般采用实时操作系统（RTOS）作为系统开发和运行支持平台，支持模块化开发，提高开发效率，缩短开发周期，便于程序的调试、维护，使实时性能得到保证，系统稳定可靠。RTOS为每个任务建立一个可执行环境，并可方便地在任务间传递消息，在中断处理程序和任务间传递事件，根据任务优先级实施抢占调度。

从实时操作系统（Real-time OS）的内核功能、实现方法和运行机制可得其目标包括：按照抢占优先级策略控制管理实时应用程序每个并发任务的运行；每个任务在多长时限可以完成或得到响应。任务时限（dead-line）是实现每个实时任务必备的性能指标。

时限可以分为硬时限（Hard Deadline）和软时限（Soft Deadline）。具有硬截止时间的任务即为关键任务，如果不能满足时限，则视为系统错误。根据任务设置的重要程度，将拥有关键任务的实时系统称为硬实时系统，否则称为软实时系统。

1.1 中断延迟

从一个外部事件发生到响应中断处理函数的第一条指令开始执行，这段时长称为中断延迟。很多实时任务由中断驱动执行，中断事件必须在限定的时限内处理，否则将产生严重后果。

1.2 抢占延迟

从一个外部事件发生到处理该事件任务的第一条指令开始执行，这段时长称为抢占延迟。大多数实时系统都是处理一些周期性或非周期性的重复事件，事件触发任务执行。每当事件发生，相应的处理任务必须及时得到调度执行，否则将无法满足时限。抢占延迟反映系统响应的及时程度。

图1表示实时软件设计编程和运行层次结构。该图对实现实时应用程序功能设计接口和运行机制进行层次划分。指明基于操作系统内核进行应用开发的编程层次和接口。从而形成实时应用程序内部结构。

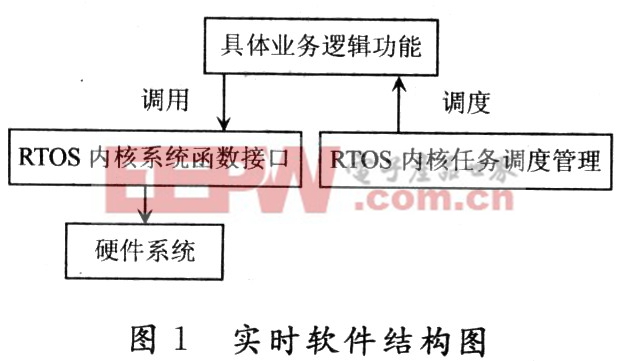
实现具体实时应用业务逻辑一般采用分解任务的方法。将一个实时应用功能划分为多个并发执行的任务。分配任务不同的优先级，赋予任务自主延迟功能，进行必要的任务通信，设置关键任务的中断响应。调用RTOS内核系统函数接口，创建实时任务；任务的运行从接受内核调度开始，按照自身流程设计循环执行，直至系统运行结束。

实时应用的基本构成单位和基本功能实现方法，如图2所示。

2 基于μC／OSⅡ内核的实时任务模型

μC／OSⅡ嵌入式操作系统是一个多任务、优先级抢占、可移植、可裁减的实时内核。具有时间、内存、信号量、邮箱和信息队列等各类功能函数，各任务间可以互相通讯，适用于小型CPU，开源代码简练，应用领域广泛。

基于μC／OSⅡ实时操作系统内核进行应用程序开发，首要的工作在于如何将应用程序中的功能进行模块分解，使每个模块转换为可并发执行的任务；调用内核完成任务流程的设计与实现；启动操作系统内核的任务调度程序，并发执行任务。

实时应用程序的开发既要考虑内核功能及接口，也要设计应用逻辑功能。设计一个任务模型，直接服务于实时应用程序的设计与实现。该模型对设计与实现的全过程进行简要分解，对各个环节进行功能设计与实现，引导用户将设计功能转换为应用程序。

图3提供了任务模型框架与构建基本步骤。

2.1 任务分解

任务分解将一个实时应用业务逻辑，按照任务的管理和控制接口划分为若干独立的任务，并发运行，实现应用功能。简单地分为设计阶段和编码阶段。

2.1.1 设计阶段

（1）根据应用程序功能需求，将应用程序功能划分为若干并发任务。首先将需要并发执行的子功能确立为任务，任务优先级按响应的迫切程度确定。

（2）确定每个任务处理流程，确保完成任务功能。

（3）确定任务功能实现是否与其他任务的执行有关联。

2.1.2 编码阶段

（1）完成每个任务的程序设计。将任务流程使用C语言编写为独立的函数。根据应用需求，不同的任务也可共用同一个函数的代码段。

（2）实时任务需确定优先级。为确保低优先级任务有机会运行，每个任务函数中需包括睡眠、挂起、等待指定时间等一些自主放弃CPU的语句，调用内核函数实现。

2.2 任务通信

实时任务间存在互相合作或竞争关系。μC／OSⅡ实时操作系统内核允许并发任务间通过事件、信号量、消息邮箱、消息队列进行通信。实现分为两步