RBF网络和贝叶斯分类器融合的人脸识别方法设计

引言

本文基于人脸图像分块和奇异值压缩，进行RBF 神经网络和贝叶斯分类器融合的设计。将人脸图像本身的灰度分布描述为矩阵，其奇异值特征具有转置不变性、旋转不变性、位移不变性、镜像不变性等诸多重要的性质，进行各种代数和矩阵变换后提取的代数特征是人脸的表征。由于整体图像的奇异值向量反映的是图像整体的统计特征，对细节的描述还不够深入，本文模拟人类识别人脸的模式，在图像分块和加权的基础上，突出待识别人脸的骨骼特征，近似于人类在识别人脸时自动剔除同一人脸的变化部位的差异能力

径向基函数（RBF）网络是一种性能良好的前馈型三层神经网络，具有全局逼近性质和最佳逼近性能，训练方法快速易行，RBF 函数还具有局部响应的生物合理性。RBF神经网络隐含层结点使用了非线性传输函数，比单层感知器网络具有更强的分类能力。在隐含层中心确定的情况下，RBF神经网络只需对隐含层至输出层的单层权值学习修正，比多层感知器具有更快的收敛速度，这也是本文选择RBF神经网络作为分类器的原因。

在 RBF 神经网络构建和初始化采取有监督的聚类算法，在网络参数的最终调整和训练方面采取 Hybrid学习（HLA）算法。在隐层参数固定的条件下，由线性最小二乘法计算隐层和输出层之间的连接权值，由梯度下降法调整隐层神经元的中心和宽度。这种混合学习算法，能使RBF网络逼近Moody准则下的最优结构，即：在没有其它先验知识的情况下，与给定样本一致的规模最小的网络就是最好的选择。从而保证该网络具有较好的泛化能力。

贝叶斯网络是一个带有概率注释的有向无环图，图中的每一个结点均表示一个随机变量，图中两结点间若存在着一条弧，则表示这两结点相对应的随机变量是概率相依的，反之则说明这两个随机变量是条件独立的。网络中任意一个结点X 均有一个相应的条件概率表（CONditional Probability Table，CPT），用以表示结点X 在其父结点取各可能值时的条件概率。若结点X 无父结点，则X 的CPT 为其先验概率分布。贝叶斯网络的结构及各结点的CPT 定义了网络中各变量的概率分布。

奇异值分解SVD

奇异值分解非常有用，对于矩阵A（m*n），存在U（m*m），V（n*n），S（m*n），满足A = U*S*V’。U和V中分别是A的奇异向量，而S是A的奇异值。AA'的正交单位特征向量组成U，特征值组成S'S，A'A的正交单位特征向量组成V，特征值（与AA'相同）组成SS'。因此，奇异值分解和特征值问题紧密联系。

奇异值分解提供了一些关于A的信息，例如非零奇异值的数目（S的阶数）和A的秩相同，一旦秩r确定，那么U的前r列构成了A的列向量空间的正交基。

对于任何一个矩阵A∈Rm×n，利用奇异值分解将其转化为对角矩阵。

设A∈Rm×n（不失一般性，设m≥n），且rank（A）=k，则存在两个酉矩阵Um×m和Un×n及广义对角阵Dm×m使下式成立：

其中U的列向量是AAT的特征向量，V的列向量是ATA的特征向量，T表示转置。

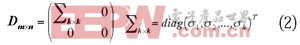
称为矩阵A的奇异值， ui（i=k+1,…,m）是AAT对应于λi=0的特征向量，vi（i=k+1,…, n）是ATA对应于λi=0的特征向量。如果矩阵A代表一幅人脸图像，则式

表示对该人脸图像进行了正交分解，将矩阵

中主对角线上的奇异值元素连同中剩余的（ri-k）个0组合构成一个n维列向量

。

由于任何实矩阵A对应唯一的奇异值对角阵

，因此，一幅人脸图像对应于唯一的奇异值特征向量。

（1）从人脸数据库选择人脸作为识别训练集；

（2）将被选入训练集的人脸图像几何归一化处理；将被选入训练集的人脸图像灰度归一处理；

（3）将预处理过的人脸图像划分成大小为的子块；

（4）将每一幅图像变为一个列向量（先分别将每一个子块所有向量排成一列，再将所有子块按顺序排成一列）；然后以子块为单位进行；

基于面部骨骼特征、眼睛的分布、鼻子的形状等结构特征，是鉴别人脸的主要依据。将每一幅人脸图像所形成的矩阵划分成…等个二维矩阵分别降维为一维列向量。求训练集中所有对应子块的平均值，

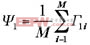
；再对每一类样本中的所有对应子块求平均，

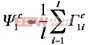
；对应子块进行样本规范化，

；

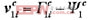并求协方差矩阵：

，

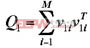从中取 m 个较大特征值对应的特征向量，构成对应子块的特征脸空间 W1 ，即W1 =[w11,w12,…,w1 m ]T 。再对训练样本进行规范化处理

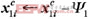
，投影到特征脸空间，获得投影特征为：

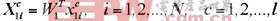
。对任一测试样本对应子块进行规范化处理，即

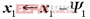
，然后得到投影特征，即

　用上述方法逐一对每个子块进行处理。得到

。

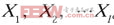
基于特征分块贝叶斯分类器设计

每个基于特征分块的贝叶斯分类器，利用了所对应的图