如何制作动画程序

的处理。此时，应该知道终端是否适应双缓冲存储器、以及是否有必要分开处理。

使用Canvas类的isDoubleBufferd()方法就能知道是否适应双缓冲存储器。由于使用这种方法可以区分开适应双缓冲存储器的情况和不适应适应的情况，因此无论在什么样的环境下都能够有效控制闪烁现象。示例如下：（ex.6）

classDoubleBufferdCanvasextendsCanvas{

ImageoffImg=null;//关闭画面的图片

/**

*表示canvas之前所运行的方法

*/

protectedvoidshowNotify(){

if(!isDoubleBuffered()){//关闭画面的图片

offImg=Image.createImage(getWidth(),getHeight());

}

}

/**

*描绘方法

*/

protectedvoidpaint(Graphicsg){

Graphicsbg=null;

if(offImg!=null){

bg=offImg.getGraphics();

}else{

bg=g;

}

//使用bg描绘

bg.setColor(255,255,255);

bg.fillRect(0,0,getWidth(),getHeight());

bg.setColor(255,0,0);

bg.drawArc(x,y,30,30,0,360);//描画圆

//将offscreenimage导入画面

if(!isDoubleBuffered()){

g.drawImage(offImg,0,0,Graphics.TOP|Graphics.LEFT);

bg=null;

}

}

}

ex.6

■制作应用程序

4-3-1时钟的应用程序

那么，现在我们就作为示范使用动画制作应用程序吧。在本讲中将要制作的应用程序就是模拟表应用程序。利用秒表，描绘出模拟表。在描绘模拟表针时使用三角函数。类结构表如下：（表2）

Table2

4-3-2时间的设定

在模拟表应用程序中秒针一秒动一下。因此，使用秒表，要设定每秒不同时刻的画面更新。在ClockCanvas类的paint方法内取得时刻，描绘钟表。秒表任务如下所示：（ex.7）

/**********************************************

*秒表任务

**********************************************/

classClockTimerTaskextendsTimerTask{

privateClockCanvascanvas;

/**

*构造函数

*/

publicClockTimerTask(ClockCanvascanvas){

this.canvas=canvas;

}

/**

*在每个指定时间内运行

*/

publicvoidrun(){

canvas.repaint();//再次描绘canvas

}

}

ex.7

定义完秒表任务后，就要在秒表上设定秒表任务。用ClockCanvas类的构造函数进行如下设定。（ex.8）

/**

*构造函数

*/

publicClockCanvas(){

//设定秒表

timer=newTimer();

timerTask=newClockTimerTask(this);

timer.schedule(timerTask,1000,1000);//Onceevery1,000ms

}

ex.8

4-3-3描画钟表

设定完秒表后开始描绘钟表。下面就是钟表的框架(clock.png)。（图4）

Figure4

接下来描画秒针。因为要根据时刻变化秒针的位置，所以有必要根据时刻计算秒针的位置。在这儿用Graphics类的drawLine方法描绘秒针。在表的中心坐标上固定住线的始点，从时刻中计算出线的终点。

使用三角函数计算秒针终点的坐标。表的中心坐标是（x,y）、秒针的长度设为1，秒针的角度设为θ，那么终点的坐标就是(x+l*cos(θ)，y+l*sin(θ))。（图5）

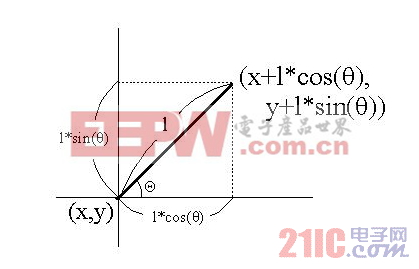
Figure5

三角函数的实际计算，在J2SE中，Math类有sin,cos方法，所以通常会使用这些方法，而J2ME中是没有这种方法的。因此，在本讲中定义了名为TrigonometricFunctions的类，将预先计算好的sin,cos值扩大10000倍排列并保持在这个类中。所谓扩大10000倍，是由于J2ME不支持double和float等小数点型，所以不能原封不动地保存小数点sin,cos。因此，用MIDP处理小数时，将小数扩大几倍变成整数加以保持，实际上在使用时，用事先乘出的数值再除以所乘的数值，计算并使用由此而得出的实际值。

然而，在J2ME下处理含有小数的数值时，由于要将小数四舍五入成整数所以就会产生误差。例如：0.12341234…四舍五入成整数就是0，这与原来的0.12341234…是有误差的。由于要尽量减少误差，所以计算之前要尽可能的乘以大数值并且有必要保存其整数。例如：在先前的0.12341234…基础上乘以1000后就变成了123.41234…，小数点以下四舍五入后就是123。将123除以1000后就是0.123。这与开始的数值之间的误差仅为0.00041234…，原封不动的将原来的数值四舍五入后数值0产生的误差是0.00041234…，二者相比则前者的误差要小的多。总之，小数上乘以的数值越大四舍五入后与原来的数值之间的误差就越小。

先讲sin,cos的数值扩大10000倍，秒针坐标计算的最后在除以10000。N800画面尺寸的纵长为180，那么进行180*x（只有X为小数）计算时的最大误差是

0.0000999...*180=0.017999...isapproximately0.0180

总是比1小，没有四舍五入的误差。

接下来描绘秒针。SecondAngle作为秒针的角度,SECOND_LENGTH是秒针的长度,表的中心坐标是(CENTER_X,CENTER_Y)。（ex.9）

intsecondX=CENTER_X+TrigonometricF