基于SoC的MPEG-4视频解码加速器

引言

随着MPEG-4应用的普及, 符合MPEG-4标准的视频在手持设备上的应用越来越广泛, SoC技术可以在完成其它功能的同时, 在手持设备上低成本低功耗的实现MPEG-4视频解码。而基于SoC的解码方案可以有多种, 例如采用CPU 内核软件解码,也可引入DSP核, 或者设计专用的硬件加速电路。但是, 软件解码在系统繁忙时难以满足实时性要求,引入DSP核会使SoC的芯片成本大为增加, 所以本文将MPEG-4的解码电路作为SoC芯片中的一个硬件加速模块来实现。

在手持设备应用中, MPEG-4 视频简单层(Simple Profile) 最为常用, 而其中计算量最大的部分是反离散余弦变换( Inverse Discrete CosineTransform ) , 所以反离散余弦变换的实现是加速MPEG-4 解码的关键。有很多优秀的设计专门以处理IDCT为目标.本文描述的MPEG-4解码加速器基于AMBA 总线, 作为高速总线(AHB) 上的一个主设备, 对四个亮度块(block) 和两个色差块组成的宏块(macrob lock) 一起做IDCT 运算, 并根据配置完成IDCT前的反量化和IDCT后运动补偿的图像叠加, 最终将结果写回显存。整个过程高度并行处理。

本文第1部分主要介绍IDCT快速算法的选择和优化, 第2部分讨论硬件结构和设计技巧, 第3部分介绍仿真验证和综合结果。

1　二维DCT?IDCT 算法描述及快速算法的选择和优化

1.1　算法描述

对于输入矩阵f (x , y ) {0≤i, j N }, 它的离散余弦变换式如下:

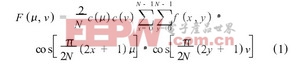
反变换式如下：

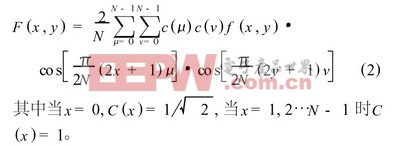
直接计算IDCT , 每个象素点f ( i, j ) 都需要计算N2次乘法, 一个块有N2 个象素点, 总共需要N4 次乘法计算, 因此计算量相当大。

1.2　快速算法的选择

二维IDCT 可以写成:

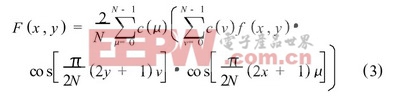
上式括号内是对F (u, v ) 的一行作一维IDCT 变换, 括号外是对行IDCT 的结果做一维列IDCT变换。如不考虑系数2/N , 二维的IDCT 就分解为对矩阵F (u, v ) 先做行IDCT 再做列IDCT 的2N 次一维IDCT 变换。(本文中取N = 8)。

对于一维IDCT 有许多优秀的快速算法。其中一种是将IDCT 原始的变换矩阵分解成几个利于计算的变换矩阵, 然后逐步计算。还有一种是利用了IDCT的奇偶对称性以及余弦函数的和差化积性质最大程度的共用乘法器。虽然后一种的乘法次数为12次, 少于前一种的16次,但由于前一种的乘法集中在输入附近, 也就是说绝大部分乘法的其中一个乘数是输入F(k ) , 因而可以通过提前判断输入F(k ) 中是否有较多的0 元素从而直接跳过一部分的乘加运算, 达到加速的目的。MPEG-4 解码的IDCT 输入中, 有大量的0, 所以前一种的算法更有利于MPEG-4 解码。其算法流程如图1。

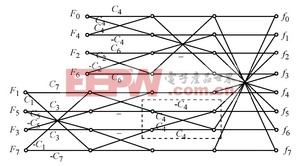
图1　chen 算法流程Ci= cos( iπ/16)

1.3　算法的优化

1.3.1　长乘法的处理

在图1的虚线中, 前一级乘加运算的结果要与C4相乘, 如果输入数据F(k ) 和系数Ci都是16位数据, 为了保证精度就要使用32 位乘16 位的乘法器,这必然成为整个电路中的关键路径, 影响其性能。若用下面的式(4) 对虚线内的条路径做变换, 虽然增加了乘法数目, 但是不仅去除掉32 位乘16 位的乘法器, 而且有利于下文将要提及的OnlyDC 和Halfzero情况的加速。

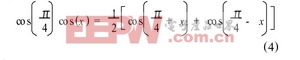
变换后的虚线内的算法流程如图2 所示。

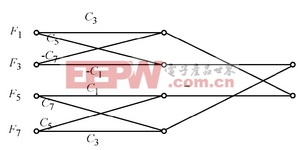
图2　chen 算法变换Ci= cos( iπ/16)

1.31.　OnlyDC 和Halfzero

本文将F(k )分为三种情况:

(1) F(k )只有F(0)为非零数据, 我们称这种情况为OnlyDC;

(2) F(k )中F(0) , F(1) , F(2) 和F(3) 为非零数据, 其他四个数据都为零, 这种情况称为Halfzero;

(3) 其它情况都归入普通情况。我们用软件直接解码的方法对典型素材作了统计(见表1) , 发现OnlyDC 和Halfzero的情况占了很大比例, 加速这两种情况的计算对加速整个视频解码的IDCT 运算有重要意义。

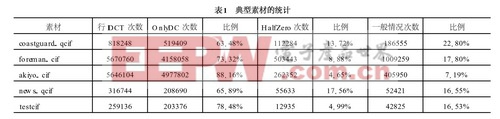
由一维IDCT 式(5) 可以看出, 对于OnlyDC 情况, f ( i) 就是F (0)/1.414 。

其中c (0) =1/1.414 ,c ( i) = 1, i= 1, 2....N - 1。如果我们把每次行和列的一维IDCT 结果放大2 倍得到f ′( i) , 对于 OnlyDC, F(0) 就是f ′( i) , 不需任何计算。这样两次一维IDCT 运算后得到的结果f ′(x , y ) 将为f (x , y ) 的2 倍, 故只要将f ′(x , y ) 右移一位就可以得到正确的f (x , y )。由图1 和图2 可以看出, 在所有的F (k ) 到f ( i) 的计算路径上, 都出现了且仅出现一次F (k ) 乘Ci, 这样我们对常数Ci 取值时直接取2cos( iπ/16), 就达到了将一维IDCT结果放大1.414倍的目的。

对于Halfzero 的情况, 可简化图1 和图2 中的F(4)、F (5)、F (6)、F (7) 的相关路径, 得到Halfzero 的算法流程(如图3)。此时时乘法总数为10 次。

图3　Halfzero 的算法流程 其中Ci = 2cos( iπ/16)

对于一般的情况, 根据图1 和图2 的流程计算,取C i = 2cos( iπ