基于Taylor展开法整定MIC-PID控制器参数
时间:03-05
来源:互联网
点击:
PID控制是迄今为止最通用的控制方法,它具有结构简单,对模型误差具有鲁棒性和易于操作等特点,仍被广泛应用于冶金、化工、电力、轻工和机械等工业过程控制中。在现有的PID参数整定方法中,Ziegler-Nichols法(简Z-N法)应用最为广泛。
内模控制(IMC)是一种实用性很强的控制方法,其设计简单,跟踪调节性能好,特别是对于鲁棒性及抗干扰性的改善和大时滞系统的控制,效果尤为显著。经过多年的发展,IMC方法的应用已经从线性系统扩展到了非线性和多变量系统,并产生了多种设计方法,如零一极点对消法,预测控制法,针对PID控制器设计的方法等。将IMC引入PID控制器的设计,既可以得到明确的解析结果,降低参数设计的复杂性和随机性,又能方便地考虑到系统鲁棒性的要求。本文针对一阶不稳定时滞过程,通过对过程控制系统含有纯滞后环节的近似处理,介绍了Taylor级数在MIC-PID参数整定中的应用,最后利用仿真进行了验证。
1 内模控制
1)内模控制原理
内模控制器与简单反馈控制结构的关系,可以用图1来表示。
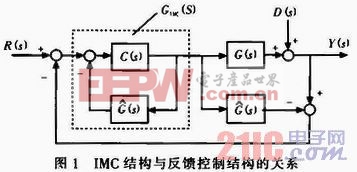
图中C(s)为反馈控制器,GIMC(s)为内模控制器,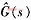 为被控过程对象,G(s)为过程对象模型,R(s)为设定值输入,D(s)为扰动输入,Y(s)为系统输出值。对于图1中的内模控制器,有:
为被控过程对象,G(s)为过程对象模型,R(s)为设定值输入,D(s)为扰动输入,Y(s)为系统输出值。对于图1中的内模控制器,有:

2)内模控制器的设计步骤

步骤2:IMC控制器设计
在设计内模控制器时,需在最小相位的 上增加滤波器,以确保系统的稳定性和鲁棒性。定义内模控制器为
上增加滤波器,以确保系统的稳定性和鲁棒性。定义内模控制器为


上面的公式可以用来求取控制器的增益、积分时间和微分时间,这些参数是过程模型参数和IMC滤波器时间常数的函数。
2 MIC-PID控制器参数的整定
设一阶不稳定时滞过程为:

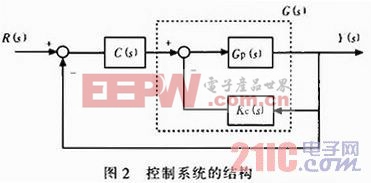
对式(20)分母中的纯滞后环节采用一阶Taylor逼近得

从式(22)可以看出纯滞后时间必须小于时间常数,即必须满足τ≤T,否则等效对象是不稳定的,由此可见,这一结果不适合大纯滞后对象。
经过内环参数整定后,内环路可以用一个等效稳定对象G(s)来代替,如果外环路采用内模控制方法,则控制系统的等效框图仍如图1所示。


这里,αa一般取O.05至0.1之间的某个常数。
3 控制过程仿真
设被控过程对象模型为: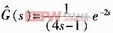 ,这里取ε=2,按式(27)、(28)、(29)整定PID参数,得K=0.344 75,Ti=3.331,TD=0.399 9;当取ε=4时,得K=0.218 3,Ti=3.164 3,TD=0.263 1。当取ε=6时,得K=0.159 4.Ti=3.081,TD=0.195 9。取α=0.05,其响应曲线如图3所示。
,这里取ε=2,按式(27)、(28)、(29)整定PID参数,得K=0.344 75,Ti=3.331,TD=0.399 9;当取ε=4时,得K=0.218 3,Ti=3.164 3,TD=0.263 1。当取ε=6时,得K=0.159 4.Ti=3.081,TD=0.195 9。取α=0.05,其响应曲线如图3所示。
设被控过程对象模型为: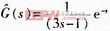 ,这里取ε=1,按式(27)、(28)、(29)整定PID参数,得K=0.725 5Ti=1.982 2,TD=0.208;当取ε=2时,得K=0.463 4,Ti=1.898 9,TD=0.137 4其响应曲线如图4所示。
,这里取ε=1,按式(27)、(28)、(29)整定PID参数,得K=0.725 5Ti=1.982 2,TD=0.208;当取ε=2时,得K=0.463 4,Ti=1.898 9,TD=0.137 4其响应曲线如图4所示。
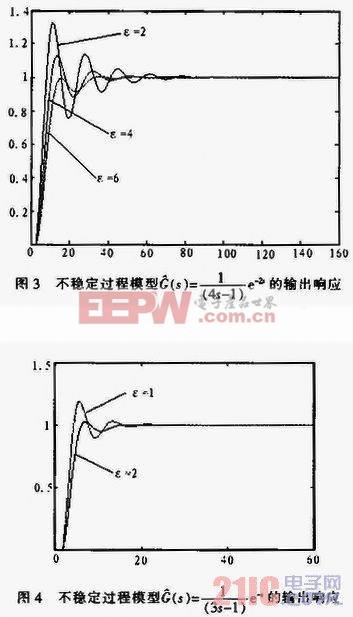
由图3和图4可见,如果纯滞后时间变小有利于系统稳定,纯滞后时间变大则系统容易发散,因此在整定参数时,可以人为地将延迟时间加大,以防止参数摄动时,系统不稳定。
4 结论
文中采用内模控制原理,针对一类不稳定时滞过程,采用双环控制结构,首先使广义对象(内环)稳定,然后按内模控制原理设计外环控制器,利用Taylor级数展开法得到了PID参数整定公式。通过仿真实例对IMC-PID控制器进行验证,结果表明在IMC-PID控制器的作用下被控系统不但具有良好的鲁棒性,而且调节快速,便于实际系统应用。
内模控制(IMC)是一种实用性很强的控制方法,其设计简单,跟踪调节性能好,特别是对于鲁棒性及抗干扰性的改善和大时滞系统的控制,效果尤为显著。经过多年的发展,IMC方法的应用已经从线性系统扩展到了非线性和多变量系统,并产生了多种设计方法,如零一极点对消法,预测控制法,针对PID控制器设计的方法等。将IMC引入PID控制器的设计,既可以得到明确的解析结果,降低参数设计的复杂性和随机性,又能方便地考虑到系统鲁棒性的要求。本文针对一阶不稳定时滞过程,通过对过程控制系统含有纯滞后环节的近似处理,介绍了Taylor级数在MIC-PID参数整定中的应用,最后利用仿真进行了验证。
1 内模控制
1)内模控制原理
内模控制器与简单反馈控制结构的关系,可以用图1来表示。

图中C(s)为反馈控制器,GIMC(s)为内模控制器,

2)内模控制器的设计步骤

步骤2:IMC控制器设计
在设计内模控制器时,需在最小相位的


上面的公式可以用来求取控制器的增益、积分时间和微分时间,这些参数是过程模型参数和IMC滤波器时间常数的函数。
2 MIC-PID控制器参数的整定
设一阶不稳定时滞过程为:


对式(20)分母中的纯滞后环节采用一阶Taylor逼近得

从式(22)可以看出纯滞后时间必须小于时间常数,即必须满足τ≤T,否则等效对象是不稳定的,由此可见,这一结果不适合大纯滞后对象。
经过内环参数整定后,内环路可以用一个等效稳定对象G(s)来代替,如果外环路采用内模控制方法,则控制系统的等效框图仍如图1所示。


这里,αa一般取O.05至0.1之间的某个常数。
3 控制过程仿真
设被控过程对象模型为:
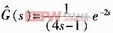 ,这里取ε=2,按式(27)、(28)、(29)整定PID参数,得K=0.344 75,Ti=3.331,TD=0.399 9;当取ε=4时,得K=0.218 3,Ti=3.164 3,TD=0.263 1。当取ε=6时,得K=0.159 4.Ti=3.081,TD=0.195 9。取α=0.05,其响应曲线如图3所示。
,这里取ε=2,按式(27)、(28)、(29)整定PID参数,得K=0.344 75,Ti=3.331,TD=0.399 9;当取ε=4时,得K=0.218 3,Ti=3.164 3,TD=0.263 1。当取ε=6时,得K=0.159 4.Ti=3.081,TD=0.195 9。取α=0.05,其响应曲线如图3所示。设被控过程对象模型为:
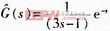 ,这里取ε=1,按式(27)、(28)、(29)整定PID参数,得K=0.725 5Ti=1.982 2,TD=0.208;当取ε=2时,得K=0.463 4,Ti=1.898 9,TD=0.137 4其响应曲线如图4所示。
,这里取ε=1,按式(27)、(28)、(29)整定PID参数,得K=0.725 5Ti=1.982 2,TD=0.208;当取ε=2时,得K=0.463 4,Ti=1.898 9,TD=0.137 4其响应曲线如图4所示。 
由图3和图4可见,如果纯滞后时间变小有利于系统稳定,纯滞后时间变大则系统容易发散,因此在整定参数时,可以人为地将延迟时间加大,以防止参数摄动时,系统不稳定。
4 结论
文中采用内模控制原理,针对一类不稳定时滞过程,采用双环控制结构,首先使广义对象(内环)稳定,然后按内模控制原理设计外环控制器,利用Taylor级数展开法得到了PID参数整定公式。通过仿真实例对IMC-PID控制器进行验证,结果表明在IMC-PID控制器的作用下被控系统不但具有良好的鲁棒性,而且调节快速,便于实际系统应用。
- 用试凑法确定PID控制器参数(12-19)
- 模糊PID控制器在伺服系统中的应用(12-12)
- Windows CE 进程、线程和内存管理(11-09)
- RedHatLinux新手入门教程(5)(11-12)
- uClinux介绍(11-09)
- openwebmailV1.60安装教学(11-12)
