伺服电机在金属切削机床上的应用

大直经的齿轮，为了减少惯量，往往在圆盘上挖出分布均匀的孔这时的惯量可以这样计算:

J=Jo+W＊R2（kg cm2）

式中:Jo为圆柱体围绕其中心线旋转时的惯量（kgcm2）

W圆柱体的重量（kg）

R旋转半径（cm）

4）相对电机轴机械变速的惯量计算将上图所示的负载惯量Jo折算到电机轴上的计算方法如下:

J=（N1/N2）2Jo

式中:N1 N2为齿轮的齿数

4.电机加速或减速时的转矩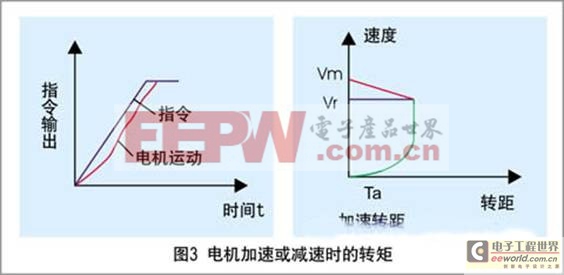


电机加速或减速时的转矩

1）按线性加减速时加速转矩计算如下:

Ta=（2πVm/60＊104） ＊1/ta（Jm+JL）（1-e-ks。ta）

Vr=Vm｛1-1/ta.ks（1-e-ksta）

Ta加速转矩（N.M）

Vm快速移动时的电机转速（r/min）

Ta加速时间（sec）

Jm电机惯量（N.m.s2）

JL负载惯量（N.m.s2）

Vr加速转矩开始减少的点

Ks伺服系统位置环增益（sec-1）

电机按指数曲线加速时的加速转矩曲线如下图: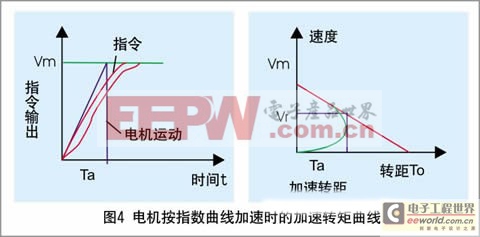



电机按指数曲线加速时的加速转矩曲线

此时，速度为零的转矩To可由下面公式给出:

To==（2πVm/60＊104） ＊1/te（Jm+JL）

Te指数曲线加减速时间常数

2）当输入阶段性速度指令时，它的速度曲线与转矩曲线如图4所示。

这时的加速转矩Ta相当于To，可由下面公式求得（ts=ks），

Ta==（2πVm/60＊104）＊1/ts（Jm+JL）。

5.工作机械频繁启动，制动时所需转矩，当工作机械作频繁启动，制动时，必须检查电机是否过热，为此需计算在一个周期内电机转矩的均方根值，并且应使此均方根值小于电机的连续转矩。电机的均方根值:

Trms=√[（Ta+Tf）2t1+Tf2t2+（Ta-Tf）2t1+To2t3]/T周

式中: Ta加速转矩（N.M）

Tf摩擦转矩（N.M）

To在停止期间的转矩（N。M）

t1t2t3t周 所知的时间可参见图5所示。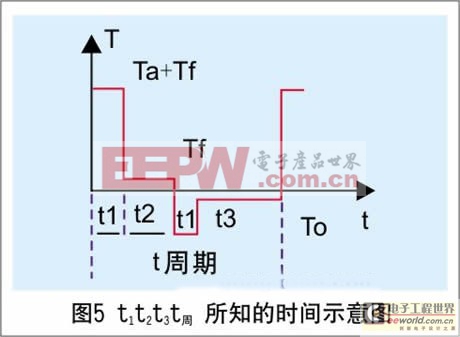


t1t2t3t周 所知的时间示意图

6.负载周期性变化的转矩计算（如图6所示），也需要计算出一个周期中的转矩均方根值Trms。且该值小于额定转矩。这样电机才不会过热，正常工作。



负载周期性变化的转矩计算图

二、负载惯量的限制

负载惯量与电机的响应和快速移动ACC/DEC时间息息相关。带大惯量负载时，当速度指令变化时，电机需较长的时间才能到达这一速度，当二轴同步插补进行圆弧高速切削时大惯量的负载产生的误差会比小惯量的大一些。

通常，当负载惯量小于电机惯量时上述提及的问题一般不会发生。如果高于5倍马达转子惯量，一般伺服会出现不良反应，像高速激光切割机床，在设计时就要考虑负载惯量低于电机转子惯量。台达伺服马达在此方面有它特有的优势，负载惯量比高，应用在此行业台达伺服的优势更为显著。