基于Matlab和Visual C++的数字滤波器设计方法

别。一般情况下，可以通过频率的预畸变进行校正。但总体来说，双线性变换法的仿真结果比脉冲响应不变法更加理想。

由于脉冲响应不变法从s平面到z平面是多值映射，会在频域响应产生混叠失真。而双线性变换法可以把整个s平面变换到整个z平面上去，且使s的左半平面映射到z平面的单位圆内，所以设计采用双线性变换法。

双线性变化法的映射函数为

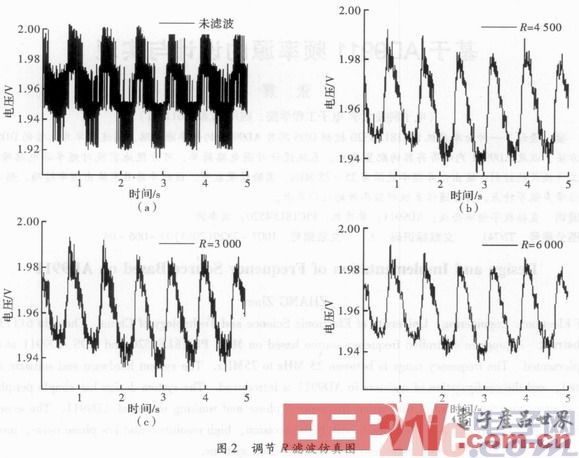
调用Matlab中的Fiher函数R1和R2调节参数、进行仿真，仿真结果如图2所示。图2(a)是未加滤波的波形，图2(b)、图2(c)、图2(d)的电阻依次增大，从图中可以看到，电阻越大，高频分量越少。

4 时域传递函数

Matlab一般只用于功能仿真，而实际项目应用，通常采用Visual C++软件编程进行信号控制和硬件实现，所以需要将Matlab仿真时使用的滤波器函数Filter转化为C代码实现。

软件编程有时域和频域两种思路。由于输入信号较为复杂不易进行时-频转换，只能采用时域滤波。所以需将传递函数反变换到时域，对信号进行滤波处理。

5 时域卷积滤波

卷积在通信技术和信号处理中起着重要的作用。在线性时域系统中，根据时间的连续性，可以分为卷积积分和卷积和。在LTI连续时间系统中，把激励信号分解为一系列冲激函数，求出各种冲激函数单独作用于系统时的冲激响应，然后将这些响应相加就得到系统对于该激励信号的零状态响应。这个相加的过程表现为求卷积积分。在LTI离散系统中，可用上述方法进行分析。由于离散信号本身是一个序列，因此，激励信号分解为单位序列的工作就较容易完成。如果系统的单位序列响应为已知，那么，也不难求得每个单位序列单独作用于系统的响应。把这些序列相加就得到系统对于该激励信号的零状态响应，这个相加的过程表现为求卷积和。

由于本系统中的信号是离散时间序列，常用的卷积和的求解方法有图解法、对位相乘求和法、解析法和列表法等4种。一般，待处理的信号的数据量比较大，列表法不适用，所以采用解析法。

卷积与傅里叶变换有着密切的关系。利用两个函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换的性质，能使傅里叶分析中许多问题的处理得到简化。本文正是采用这一点，将频域的滤波转化为时域滤波。

频域相乘等效于时域卷积。编写C程序求输入信号和传递函数的卷积和。当两个信号为因果信号时，可以根据式(5)求卷积和。当f1(k)的数据长度为m;f2(k)的数据长度为n(n

6 结果及分析

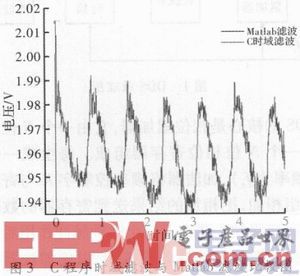
信号分别经卷积和滤波和Filter函数滤波，将滤波后的数据导入Matlab比较，结果如图3所示。由图可见，前者在初始状态出现尖峰，这是因为卷积和是在特定窗口内时域累加的过程，会造成头部数据和尾部数据不准确。虽然编写的C卷积和滤波程序有一定的缺陷，但是整体波形一致，说明实验获得初步成功。

7 结束语

提出了一种将硬件滤波电路数字化的方法，并在Matlab和Visual C++平台上得以实现。与模拟滤波电路和传统的数字滤波相比，不仅比传统的数字滤波算法简单快捷，而且有效防止了模拟电路中器件的寄生参数、精度、温度等的影响，使滤波更加稳定。