小波变换和motion信号处理：第二篇

ion，如下图所示：

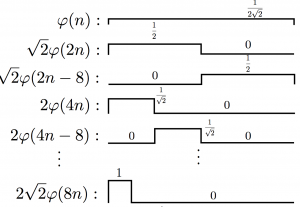
上图就是四个子空间的basis集合的展览。通过前面的讨论，我们还知道，一开始的scaling function可以通过更精细的子空间的scaling function(它们都是对应子空间的basis)来构建。比如

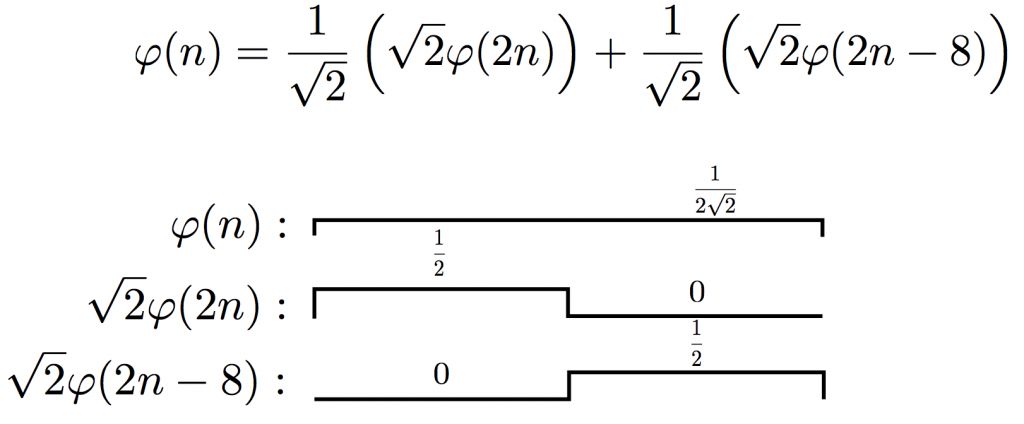
对于更加finer的scale：

图2

依此类推。实际上，对于任何scale和translate过的scaling function，都可以用更加精细的scale层面上的scaling function构建出来。

然后，我们有各种scale下的scaling function了，该看看它们分别所对应的嵌套的空间序列

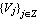
了。先看看V0，自然就是以基本的scaling function为基础去SPAN出来的：

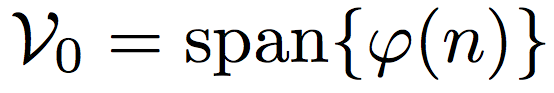
这个不新鲜，刚才就讲过了。这个子空间代表什么样的信号?常量信号。道理很简单，这个scaling function在整个信号长度上，没有任何变化。继续往下看：

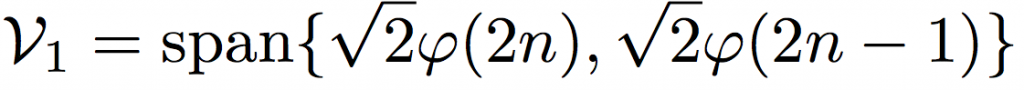
这个相比V0更加finer的子空间，代表着这样一种信号，它从1-4是常量，从5-8是另一个常量。同理我们有：

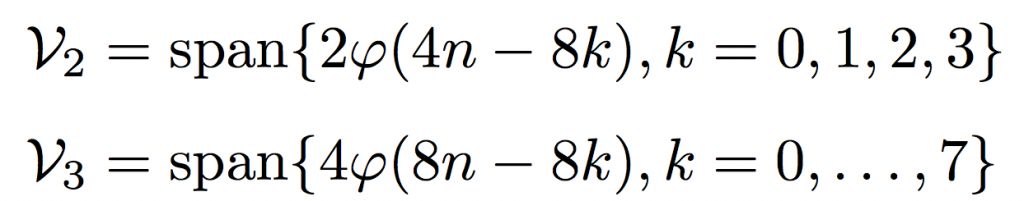
V2代表的信号，是分别在1，2; 3，4; 5，6; 7，8上有相同值的信号。那么V3呢?则表示任何信号，因为对于V3来讲，任何一个时间刻度上的值都可以不一样。而且现在，我们也可以通过上面的一些scaling functions的波形验证了之前提到的多解析度分析中的一个核心性质，那就是：

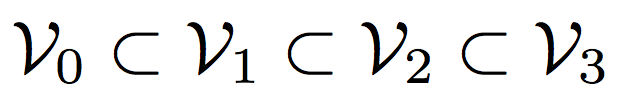
我们之前讲了一堆多解析度的理论，但直到现在，通过这些图形化的分析，我们可能才会真正理解它。那好，既然我们有一个现成的信号，那就来看看，对这个信号作多解析度分析是啥样子的：

你看，在不同的子空间，对于同一个信号就有不同的诠释。诠释最好的当然是V3，完全不损失细节。这就是多解析度的意义。我们可以有嵌套的，由scaling function演变的basis function集合，每一个集合都提供对原始信号的某种近似，解析度越高，近似越精确。

说到这里，可能你对scaling function以及多解析度分析已经比较理解了。但是，我们还没有涉及到它们在小波变换中的具体应用，也就是还没有回答刚才那个问题：凭空插了一个scaling function到小波basis组合中干嘛。也就是说，我们希望理解scaling function是怎么和小波函数结合的呢，多解析度能给小波变换带来什么样的好处呢。这其实就是是小波变换中的核心知识。理解了这个，后面的小波变换就是纯数学计算了。

好，我们已经知道，对于子空间V0，basis是scaling function：

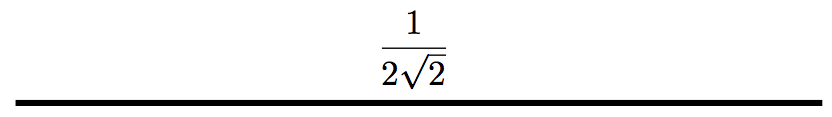
对应的小波函数是：

然后子空间V1的basis集合是这俩哥们：

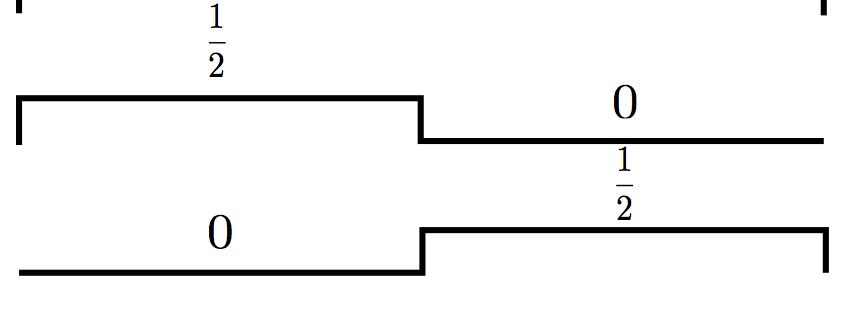
看出什么规律了么?多看几次这三个图，你会惊讶地发现，在V0中的scaling function和wavelet function的组合，其实就是V1中的basis!继续这样推导，V1本来的的basis是：

然后V1中对应的wavelet function是

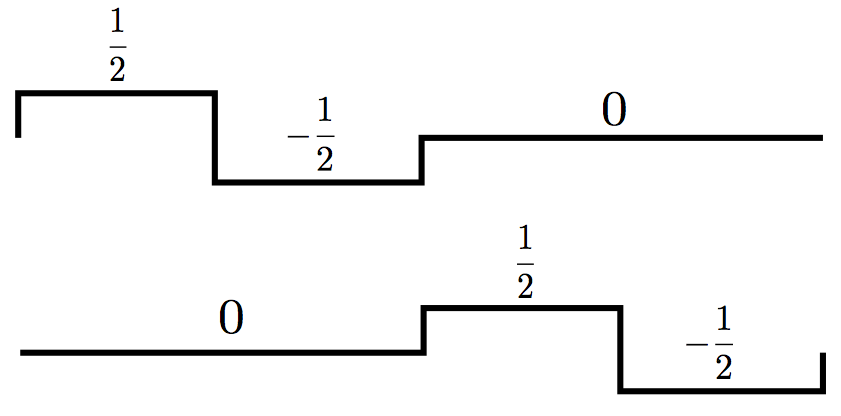
他们的组合，本质上也就是V2的basis(参考图2)。你继续推导下去，会得到同样的结论：在scale j的wavelet function，可以被用来将Vj的basis扩展到V(j+1)中去!这是一个非常非常关键的性质，因为这代表着，对任何一个子空间Vj，我们现在有两种方法去得到它的orthonormal basis：

1. 一种就是它本来的basis

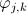
，对任意k。

2. 第二种就是它上一个子空间的basis

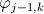
，对任意k，以及上一级子空间的wavelet function

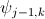
，对任意k。

第二种选择能给我们带来额外的好处，那就是我们可以循环不断地用上一级子空间的scaling function以及wavelet function的组合来作为当前子空间的基。换句话说，如果针对V3这个子空间，它实际上就有四种不同的，但是等价的orthonormal basis：

1. 本级(V3)的scaling function basis set

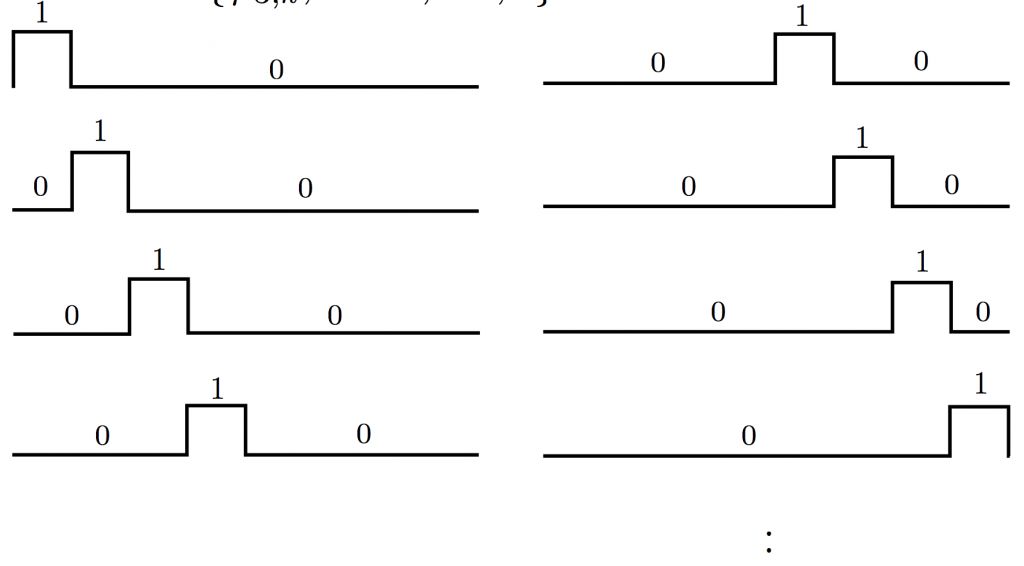
2. 上一级(V2)的scaling function + wavelet function;

3 . 上上一级(V1)的scaling function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function;

4. 上上上一级(V0)的scaling function + 上上上一级(V0)的wavelet function + 上上一级(V1)的wavelet function + 上一级(V2)的wavelet function

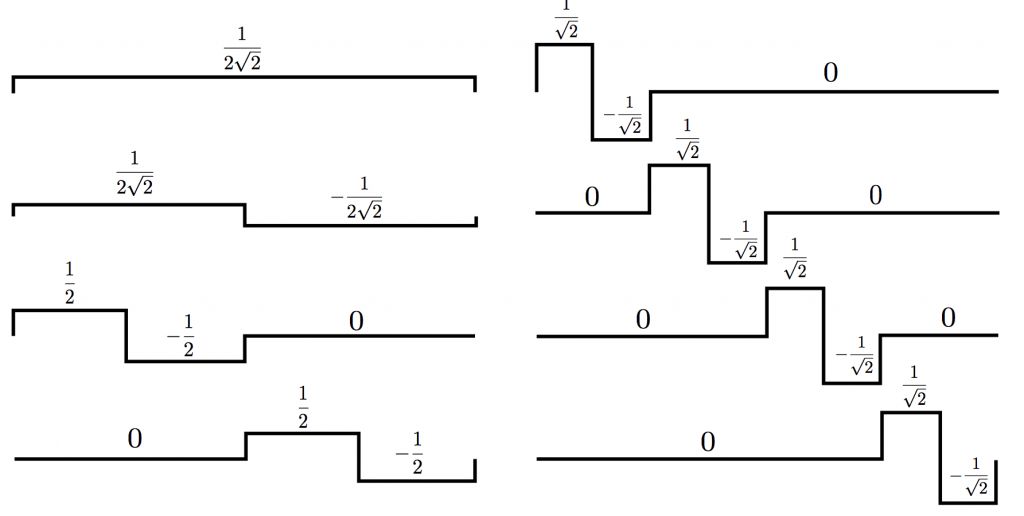
好，看看最后一种选取方式，有没有感到眼熟?对了，它就是我们之前提到的“针对此信号space的哈尔小波basis组合”，参见图1。现在我们知道了，这个scaling function不是凭空插进去的，而是通过不断的嵌套迭代出来的：)

那为什么我们最后选定的是这种选取方式呢?实际上，刚才介绍的这个性质已经告诉我们，对于任何的scale j0，我们都可以给我们的signal space找到一组orthonormal basis，这个basis是通过组合scale j0上的scaling function以及所有在scale j，j>j0上的wavelets得到的。这样，基于这个orthonormal basis，所有信号空间中的信号都可以写成组成这个basis的